Thorsten Reinecke
Der (p-1)-Algorithmus zur Faktorisierung natürlicher Zahlen basiert auf dem sogenannten kleinen Fermatschen Satz:
![]() prim
prim
![]() für
für
![]()
Dieser Sachverhalt wird häufig für Vorstufen verschiedener Primzahltests verwendet,
in dem man für verschiedene Basen
![]() berechnet. Falls der
Ausdruck ungleich 1 wird, weiß man, daß die Zahl zusammengesetzt sein muß. Andernfalls
``verstärkt'' sich die Annahme, daß die Zahl prim sein könnte.
berechnet. Falls der
Ausdruck ungleich 1 wird, weiß man, daß die Zahl zusammengesetzt sein muß. Andernfalls
``verstärkt'' sich die Annahme, daß die Zahl prim sein könnte.
Der kleine Fermatsche Satz läßt sich jedoch auch zur Faktorisierung natürlicher
Zahlen einsetzen. Nehmen wir an, ![]() wäre unser gesuchter Primfaktor. Nehmen
wir ferner an, wir hätten bereits für kleinere Primfaktoren Probedivision durchgeführt.
Dann zerfällt
wäre unser gesuchter Primfaktor. Nehmen
wir ferner an, wir hätten bereits für kleinere Primfaktoren Probedivision durchgeführt.
Dann zerfällt ![]() in mindestens zwei Faktoren:
in mindestens zwei Faktoren:
![]() .
Mit einiger Wahrscheinlichkeit ist
.
Mit einiger Wahrscheinlichkeit ist
![]() sogar noch weiter zerlegbar.
Und genau diese Hoffnung hegt man bei der (p-1)-Faktorisierungsmethode. Man
rät sukzessive mögliche kleine Faktoren von
sogar noch weiter zerlegbar.
Und genau diese Hoffnung hegt man bei der (p-1)-Faktorisierungsmethode. Man
rät sukzessive mögliche kleine Faktoren von ![]() .
.
Seien
![]() diese gewählten Zahlen und
diese gewählten Zahlen und ![]() eine gewählte Basis, dann wäre
eine gewählte Basis, dann wäre
![]() .
Dies läßt sich mit den Potenzgesetzen umformulieren zu
.
Dies läßt sich mit den Potenzgesetzen umformulieren zu
![]() .
Nun sieht man auch, daß falsch geratene Faktoren von
.
Nun sieht man auch, daß falsch geratene Faktoren von ![]() die Kongruenz
trotzdem erhalten, da die Basis
die Kongruenz
trotzdem erhalten, da die Basis ![]() unter den oben genannten Einschränkungen
beliebig gewählt werden kann, somit also falsche
unter den oben genannten Einschränkungen
beliebig gewählt werden kann, somit also falsche ![]() in die Basis gezogen
werden können.
in die Basis gezogen
werden können.
Ein Problem verbleibt allerdings noch: Da wir ![]() nicht kennen, können
wir die Kongruenz nicht bilden. Dies stört allerdings wenig, da für eine gegebene
Zahl
nicht kennen, können
wir die Kongruenz nicht bilden. Dies stört allerdings wenig, da für eine gegebene
Zahl
![]() , deren Faktor
, deren Faktor ![]() wir suchen, folgendes gilt:
wir suchen, folgendes gilt:
![]() .
.
Falls
![]() gilt, so gilt
gilt, so gilt
![]() und somit
und somit
![]() . Wenn
nun
. Wenn
nun ![]() ist (und dies ist ein sehr wahrscheinlicher Fall!), so erhalten
wir durch
ist (und dies ist ein sehr wahrscheinlicher Fall!), so erhalten
wir durch
![]() den gewünschten
Teiler
den gewünschten
Teiler ![]() .
.
Ein praktikabler Algorithmus ergibt sich daraus, in dem man sich eine Basis
![]() wählt und dann alle Primzahlen (und ggf. Primzahlpotenzen) bis zu einer
vorher festgelegten Obergrenze als Exponenten verwendet. In regelmäßigen Abständen
testet man dann den ggT von
wählt und dann alle Primzahlen (und ggf. Primzahlpotenzen) bis zu einer
vorher festgelegten Obergrenze als Exponenten verwendet. In regelmäßigen Abständen
testet man dann den ggT von ![]() und
und ![]() . - Der in der Literatur
manchmal beschriebene Akkumulationsschritt, bei welchem nach jedem Exponentiationsschritt
die neu erhaltene Basis um eins vermindert mit einer Sammelvariablen zu multiplizieren
ist, um den ggT-Test anschließend mit der Sammelvariablen durchführen zu können,
ist aufgrund des Kleinen Fermatschen Satzes unnötig. Nichts desto trotz kann
die Akkumulation in vielen anderen Algorithmen die kostenintensiven ggT-Berechnungen
erheblich reduzieren und ist auch bei der Bestimmung multiplikativer, von einander
unabhängiger Inversen vorteilhaft einsetzbar.
. - Der in der Literatur
manchmal beschriebene Akkumulationsschritt, bei welchem nach jedem Exponentiationsschritt
die neu erhaltene Basis um eins vermindert mit einer Sammelvariablen zu multiplizieren
ist, um den ggT-Test anschließend mit der Sammelvariablen durchführen zu können,
ist aufgrund des Kleinen Fermatschen Satzes unnötig. Nichts desto trotz kann
die Akkumulation in vielen anderen Algorithmen die kostenintensiven ggT-Berechnungen
erheblich reduzieren und ist auch bei der Bestimmung multiplikativer, von einander
unabhängiger Inversen vorteilhaft einsetzbar.
Falls der Grundalgorithmus versagt, kann man eine zweite Phase anhängen. Diese
zweite Phase ist erfolgreich, wenn ![]() durch den Grundalgorithmus bis
auf einen Primfaktor zerlegt werden konnte. Dieser übriggebliebene Restfaktor
durch den Grundalgorithmus bis
auf einen Primfaktor zerlegt werden konnte. Dieser übriggebliebene Restfaktor
![]() kann nun ohne teure Exponentiation ermittelt werden, in dem man ein
kann nun ohne teure Exponentiation ermittelt werden, in dem man ein
![]() mit einer Primzahl
mit einer Primzahl ![]() in der Größenordnung des vermuteten
in der Größenordnung des vermuteten
![]() bestimmt und mittels Multiplikation die Umgebung von
bestimmt und mittels Multiplikation die Umgebung von ![]() nach
nach
![]() absucht. Hierfür kann man sich eine Tabelle kleiner Potenzen von
absucht. Hierfür kann man sich eine Tabelle kleiner Potenzen von ![]() anlegen, um die Abstände zwischen den Primzahlen jeweils durch eine Multiplikation
überwinden zu können:
anlegen, um die Abstände zwischen den Primzahlen jeweils durch eine Multiplikation
überwinden zu können:
![]() . Diese Phase
schließt erfolgreich ab, falls
. Diese Phase
schließt erfolgreich ab, falls ![]() und somit
und somit
![]() den Teiler liefert. Man beachte, daß die Basis
den Teiler liefert. Man beachte, daß die Basis ![]() nicht die Ursprungsbasis
ist, sondern die nach Abschluß des Standard-Algorithmus erhaltene Basis.
nicht die Ursprungsbasis
ist, sondern die nach Abschluß des Standard-Algorithmus erhaltene Basis.
Wenn man so will, kann man die Operationen als Ringoperationen auffassen. Phase 1 hat den Ring komprimiert (die Standard-Exponentiation auf den natürlichen Zahlen entspricht der multiplikativen Ring-Operation). In Phase 2 sucht man den komprimierten Ring durch additive Operationen ab.
In der Literatur sind weitere, wesentlich effizientere Methoden für Phase 2 als die hier beschriebene standard continuation entwickelt worden.
In der Literatur finden sich für die erste Phase eigentlich keine Verbesserungsvorschläge.
Wenn man den (p-1)-Algorithmus nur ergänzend zu anderen Algorithmen einsetzt, dann wird man Phase 1 möglichst kurz halten und darauf spekulieren, den Teiler in Phase 2 zu ermitteln zu können. Falls auch Phase 2 versagt, dann war die Zahl eben nicht für den (p-1)-Algorithmus geeignet. - Diese Vorgehensweise ist durchaus legitim.
Ein möglicher Nachteil des oben beschriebenen Vorgehens liegt allerdings darin, die Phase 1 zu früh abzubrechen. Eine zu große Verlängerung der Phase 1 hingegen kostet unnötige Zeit.
Eine Lösung bestünde darin, die Phase 1 substantiell zu beschleunigen. Dies ist bisher nicht gelungen.
Eine abgeschwächte Verbesserung der Phase 1 wäre erreichbar, wenn man die Phase 1 mit geringen Kosten um Elemente der Phase 2 ergänzen könnte. Die Phase 1 könnte dann mit einer wesentlich höheren Obergrenze durchlaufen werden, weil quasi parallel eine Art ``Phase 2'' abläuft. Basierend auf dem Grundalgorithmus ist dies tatsächlich möglich und die zusätzlichen Kosten sind mit denen der standard-continuation vergleichbar. Ob sich allerdings die Modifikationen lohnen, bedarf weiterer Untersuchungen. Hier bin ich eher skeptisch, da man die (p-1)-Methode - wenn überhaupt - dann nur ergänzend vor den elliptischen Kurven und/oder dem Quadratischen Sieb einsetzt. Dadurch dominiert von der Bedeutung her die Phase 2.
In einer Standalone-Anwendung des (p-1)-Verfahrens würde hingegen Phase 1 dominieren, da man nicht riskieren könnte, das Verfahren mit Phase 2 erfolglos zu beenden.
Die erforderlichen Modifikationen sind relativ simpel. Wir betrachten die fortlaufenden
Werte der Basis als Folge, die durch den Startwert ![]() und eine Folge
von Exponenten
und eine Folge
von Exponenten ![]() bestimmt werden:
bestimmt werden:
![]() .
Wir definieren ferner
.
Wir definieren ferner ![]() für negative
für negative ![]() .
.
Das (p-1)-Standardverfahren sieht dann etwa folgendermaßen aus:
![]() ; repeat
; repeat ![]() until
until
![]() ;
;
Das modifizierte Verfahren sieht so aus:
![]() ; repeat
; repeat
![]() ;
; ![]() until
until
![]() ;
;
Das modifizierte Verfahren ergänzt das Standardverfahren um zusätzliche Faktoren,
da für ![]() z.B.
z.B.
![]()
gilt und somit ein Teiler ![]() lediglich eine Auswertung später
entdeckt wird. Hingegen können zusätzliche Faktoren durch den Summenausdruck
hinzukommen, die bei jedem Auswertungsschritt variieren. Über die Höhe des Delta
kann die Größe des zusätzlichen Faktors eingestellt werden. Dieser dürfte seinerseits
mit einiger Wahrscheinlichkeit in weitere Primfaktoren zerfallen. Auf diese
Weise erhält man eine Art ``Phase 2'' bereits innerhalb der Grundphase.
lediglich eine Auswertung später
entdeckt wird. Hingegen können zusätzliche Faktoren durch den Summenausdruck
hinzukommen, die bei jedem Auswertungsschritt variieren. Über die Höhe des Delta
kann die Größe des zusätzlichen Faktors eingestellt werden. Dieser dürfte seinerseits
mit einiger Wahrscheinlichkeit in weitere Primfaktoren zerfallen. Auf diese
Weise erhält man eine Art ``Phase 2'' bereits innerhalb der Grundphase.
Allgemein gilt:
![]()
Der obige Term sieht relativ kompliziert aus; tatsächlich geht es jedoch nur um den Nachweis der Tatsache, daß das Verfahren durch Berechnung der linken Seite auch bei anderen Deltawerten zusätzliche Faktoren (rechte Seite) gegenüber dem Standardverfahren produziert.
Die zusätzlichen Kosten der Modifikation der Phase 1 sind relativ gering. Es
ist ein Ringpuffer für die Basen anzulegen. Dieser kann als Array der Größe
![]() realisiert werden. Der Zugriff erfolgt dann über die Indices
modulo
realisiert werden. Der Zugriff erfolgt dann über die Indices
modulo ![]() .
.
Nehmen wir an,
![]() bestehe aus zwei annähernd gleichen Teilern.
- Dies ist der einzige Sonderfall, wo die Fermatmethode den anderen Faktorisierungsmethoden
deutlich überlegen ist.
bestehe aus zwei annähernd gleichen Teilern.
- Dies ist der einzige Sonderfall, wo die Fermatmethode den anderen Faktorisierungsmethoden
deutlich überlegen ist.
Vorausgesetzt, daß ![]() und
und ![]() große Primzahlen sind, läßt sich auch
hier eine modifizierte (p-1)-Methode anwenden.
große Primzahlen sind, läßt sich auch
hier eine modifizierte (p-1)-Methode anwenden.
Wir gehen zunächst von folgender Kongruenz aus:
![]()
Dies ergibt umgeformt:
![]()
Nun gilt
![]() und wir erhalten
und wir erhalten
![]() .
.
Dies kann man benutzen, um ![]() zu bestimmen. Daraus wiederum können p
und q folgendermaßen berechnet werden:
zu bestimmen. Daraus wiederum können p
und q folgendermaßen berechnet werden:
Aus den binomischen Formeln ergibt sich:
![]()
also:
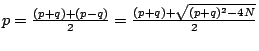
Nun gibt mehrere Alternativen, ![]() zu ermitteln:
zu ermitteln:
Wir berechnen
![]() und wandern per Division durch 2 abwärts, bis wir 1 erhalten. Dies ist über
Shiften der Werte mit geringem Aufwand möglich. Die Anzahl der Shift-Operationen
zählen wir und erhalten dadurch den Wert
und wandern per Division durch 2 abwärts, bis wir 1 erhalten. Dies ist über
Shiften der Werte mit geringem Aufwand möglich. Die Anzahl der Shift-Operationen
zählen wir und erhalten dadurch den Wert ![]() .
.
Wir wählen ein ![]() und eine Größe step. Wir berechnen für
und eine Größe step. Wir berechnen für
![]() eine Tabelle mit
eine Tabelle mit
![]() . Anschließend
können wir in sukzessive
. Anschließend
können wir in sukzessive
![]() berechnen, bis der Wert in der
Tabelle gefunden wird.
berechnen, bis der Wert in der
Tabelle gefunden wird.
Zunächst einmal ist ![]() eine gerade Zahl, was es ermöglicht, die Schrittweiten
zu verdoppeln.
eine gerade Zahl, was es ermöglicht, die Schrittweiten
zu verdoppeln.
Eine weitere Verbesserung läßt sich erzielen, wenn man berücksichtigt, daß man
rund die Hälfte der Primzahlen als Teiler von ![]() ausschließen kann.
Denn
ausschließen kann.
Denn
![]()
![]() . Eine anschließende
Multiplikation mit
. Eine anschließende
Multiplikation mit ![]() ergibt
ergibt
![]() , so daß
, so daß ![]() ein quadratischer Rest modulo
ein quadratischer Rest modulo ![]() sein muß.
sein muß.
Die Methode funktioniert nur in Spezialfällen: Die zu faktorisierende Zahl muß aus genau zwei Primzahlen bestehen. Akzeptable Laufzeiten ergeben sich nur, wenn beide Primzahlen gleichstellig sind und überdies in einer möglichst langen Kette ihrer führenden Stellen übereinstimmen.
Wenngleich es unwahrscheinlich erscheint, auf diese Weise einen Teiler zu finden, so ist doch für diesen Spezialfall die Verwandtschaft zur Faktorisierungsmethode nach Fermat ein interessanter Aspekt.
This document was generated using the LaTeX2HTML translator Version 2002-2-1 (1.70)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -transparent -white -antialias -html_version 4.0 -split 0 -nonavigation p-1.tex
The translation was initiated by Thorsten Reinecke on 2003-03-06