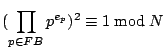
Thorsten Reinecke
Date: 2000-02-02
Für die effiziente Implementierung des Quadratischen Siebs zur Faktorisierung natürlicher Zahlen (und darauf aufbauender Verfahren wie des multipolynomialen Siebs) ist es erforderlich, die zu faktorisierende Zahl mit einem Vorfaktor zu multiplizieren. Je nach gewähltem Vorfaktor sind andere Primzahlen in der Faktorbasis enthalten.
Nach Abschluß des Quadratischen Siebverfahrens erhält man (grob vereinfacht ausgedrückt) eine nichttriviale quadratische Kongruenz zu 1 modulo der zu faktorisierenden Zahl, die als Produkt von Primzahlpotenzen der Faktorbasis angegeben ist.
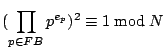
Aus Umformung der Kongruenz und Bestimmung des größten gemeinsamen Teilers erhält man schließlich einen (nicht notwendigerweise primen) Teiler der zu faktorisierenden Zahl N:
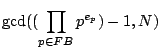
Prinzipiell ist jede genügend große Faktorbasis zur Ermittlung der quadratischen Kongruenz geeignet. Da zur Ermittlung der quadratischen Relationen allerdings ein hoher Siebaufwand erforderlich ist, wäre es wünschenswert, dem Siebverfahren eine Faktorbasis zugrunde zu legen, mit der man möglichst schnell möglichst viele Relationen ermitteln kann.
Die Quadratischen Kongruenzen, aus denen die Primfaktorzerlegungen, die innerhalb der Faktorbasis aufgehen, bestimmt werden, definieren sich bei der einfachen Version des Quadratischen Siebes durch
Hierbei entsteht jedoch ein Zielkonflikt, da man lediglich über die Wahl des Vorfaktors die Faktorbasis variieren kann, ein hoher Vorfaktor jedoch ceteris paribus den Siebaufwand vergrößert.
Die erweiterte Faktorbasis bei verschiedenen Vorfaktoren k bestimmt sich für eine zu faktorisierende Zahl N wie folgt:1
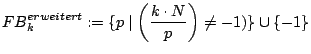
Die im Rahmen der Faktorisierung verwendeten (statischen) Faktorbasen
![]() haben dabei eine vorher festgesetzte,
von
haben dabei eine vorher festgesetzte,
von ![]() abhängige, endliche Kardinalität und bestehen (üblicherweise)
aus den den diesbezüglich kleinsten positiven Elementen von
abhängige, endliche Kardinalität und bestehen (üblicherweise)
aus den den diesbezüglich kleinsten positiven Elementen von
![]() .2
.2
Man kann also davon ausgehen, daß etwa die Hälfte der in einem für die Faktorbasis relevanten Intervall vorkommenden Primzahlen quadratische Reste liefern und damit auch Elemente dieser Faktorbasis sind. - Als einzige Einflußmöglichkeit auf die Faktorbasis verbleibt dann der Vorfaktor k.
Wenn ![]()
![]() teilerfremd zu
teilerfremd zu ![]() ist, so erhalten
wir zwei Siebtreffer in einem Siebintervall der Größe
ist, so erhalten
wir zwei Siebtreffer in einem Siebintervall der Größe ![]() , andernfalls
lediglich einen Treffer. Nicht nur die Größe, sondern auch die Teilbarkeitsstruktur
von
, andernfalls
lediglich einen Treffer. Nicht nur die Größe, sondern auch die Teilbarkeitsstruktur
von ![]() hat also Einfluß auf die Güte der zugehörigen Faktorbasis.
hat also Einfluß auf die Güte der zugehörigen Faktorbasis.
Wir gehen nun von der realistischen Grundannahme aus, daß alle Primzahlen
der Faktorbasis im Siebintervall jeweils gleichverteilt mit einer
Wahrscheinlichkeit von jeweils
![]() teilen, sofern
teilen, sofern ![]() und
und ![]() teilerfremd sind. Jeder Siebtreffer wird dabei mit
einem Trefferbonus von
teilerfremd sind. Jeder Siebtreffer wird dabei mit
einem Trefferbonus von ![]() gewichtet.
gewichtet.
Auf diese Weise erhalten wir für eine vollständig in der Faktorbasis
aufgehenden Relation folgende Äquivalenz (wobei ![]() die gesiebten
Primteiler,
die gesiebten
Primteiler, ![]() deren Exponenten darstellen):
deren Exponenten darstellen):
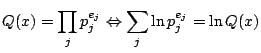
Für das Siebverfahren wird typischerweise anstelle von ![]() ein einheitlicher Schwellwert für ein komplettes Siebintervall gewählt,
um den Berechnungsaufwand klein zu halten. Ein geeigneter Schwellwert
läßt dann das Vorkommen weiterer nichtgesiebter Primzahlpotenzen sowie
einiger Primzahlen (sog. Large-Primes, Double-Large-Primes, etc.)
außerhalb der Faktorbasis zu, die bei Erreichen des Schwellwertes
durch Probedivision ermittelt werden. Der Schwellwert ist dabei so
zu bestimmen, daß der Anteil ungeeigneter Relationen, die verworfen
werden müssen, nicht ins Gewicht fällt.
ein einheitlicher Schwellwert für ein komplettes Siebintervall gewählt,
um den Berechnungsaufwand klein zu halten. Ein geeigneter Schwellwert
läßt dann das Vorkommen weiterer nichtgesiebter Primzahlpotenzen sowie
einiger Primzahlen (sog. Large-Primes, Double-Large-Primes, etc.)
außerhalb der Faktorbasis zu, die bei Erreichen des Schwellwertes
durch Probedivision ermittelt werden. Der Schwellwert ist dabei so
zu bestimmen, daß der Anteil ungeeigneter Relationen, die verworfen
werden müssen, nicht ins Gewicht fällt.
Für die Bestimmung der Qualität einer zu ![]() gehörigen Faktorbasis
sollte die mittlere Summe der Trefferboni an jeder Stelle im Siebintervall
unter den o.g. Annahmen maximiert werden.
gehörigen Faktorbasis
sollte die mittlere Summe der Trefferboni an jeder Stelle im Siebintervall
unter den o.g. Annahmen maximiert werden.
Als geeignete Qualitätsfunktion setzen wir also an:
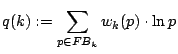
Als Vorfaktoren kommen ferner nur quadratfreie Zahlen in Frage, da die k teilenden Quadrate die Faktorbasis nicht positiv beeinflussen und damit den Vorfaktor unnötig erhöhen.3
Falls
![]() , so gilt4
, so gilt4
![]() . Andernfalls
teilen die höheren Potenzen von
. Andernfalls
teilen die höheren Potenzen von ![]() nicht und
nicht und
![]() .
.
Für den theoretischen Optimalwert ![]() nehmen wir die theoretisch
bestmögliche Faktorbasis
nehmen wir die theoretisch
bestmögliche Faktorbasis ![]() an, die aus direkt aufeinanderfolgenden
Primzahlen besteht und setzen zusätzlich
an, die aus direkt aufeinanderfolgenden
Primzahlen besteht und setzen zusätzlich
![]() :
:
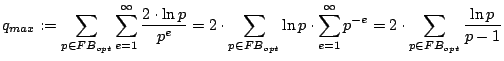
Mit ![]() haben wir einen Referenzwert, an dem wir die tatsächliche
Qualität der Faktorbasen messen können.
haben wir einen Referenzwert, an dem wir die tatsächliche
Qualität der Faktorbasen messen können.
Für eine geeignete Bewertungsfunktion müssen wir den Schwellwert,
den wir in etwa mit
![]() (
(![]() ist die Größe
des festgelegten Siebintervalls) bzw. idealisiert mit
ist die Größe
des festgelegten Siebintervalls) bzw. idealisiert mit
![]() ansetzen, berücksichtigen. Die Bewertungsfunktion ergibt sich somit
als
ansetzen, berücksichtigen. Die Bewertungsfunktion ergibt sich somit
als
Diese Bewertungsfunktion ist bezüglich ![]() simulativ zu minimieren.
Zunächst setzen wir dazu eine Größe
simulativ zu minimieren.
Zunächst setzen wir dazu eine Größe ![]() fest, die bestimmt,
wie viele Primzahlen in den zu simulierenden Faktorbasen enthalten
sein sollen. Dann bestimmen wir
fest, die bestimmt,
wie viele Primzahlen in den zu simulierenden Faktorbasen enthalten
sein sollen. Dann bestimmen wir ![]() und anschließend für aufsteigende
Vorfaktoren
und anschließend für aufsteigende
Vorfaktoren ![]() . Wir brechen die Simulation ab, wenn sichergestellt
ist, daß höhere
. Wir brechen die Simulation ab, wenn sichergestellt
ist, daß höhere ![]() nicht mehr zu einem minimalen
nicht mehr zu einem minimalen ![]() führen
können. Hierzu ist für jeden bisher bestimmten besten Vorfaktor
führen
können. Hierzu ist für jeden bisher bestimmten besten Vorfaktor ![]() die Obergrenze
die Obergrenze ![]() zu berechnen, ab der die Simulation abgebrochen
werden kann. Diese Obergrenze ist bei
zu berechnen, ab der die Simulation abgebrochen
werden kann. Diese Obergrenze ist bei
![]() erreicht:
erreicht:
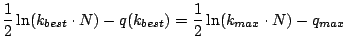
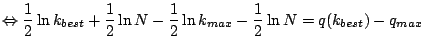
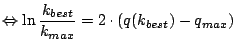
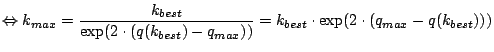
Wie man also sieht, ist diese Obergrenze nur noch indirekt über die
Faktorbasis von der zu faktorisierenden Zahl ![]() abhängig. Anstelle
der Bewertungsfunktion
abhängig. Anstelle
der Bewertungsfunktion ![]() kann deshalb auch eine modifizierte Bewertungsfunktion
kann deshalb auch eine modifizierte Bewertungsfunktion
![]() verwendet werden:
verwendet werden:
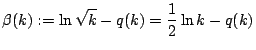
In der Praxis dürfte für größere zu simulierende Faktorbasisgrößen
![]() die Bedingung
die Bedingung ![]() unnötig hoch ausfallen. Denn
es ist dann unwahrscheinlich, daß für große Faktorbasen alle Primzahlen
in Folge enthalten sind. Der Wert
unnötig hoch ausfallen. Denn
es ist dann unwahrscheinlich, daß für große Faktorbasen alle Primzahlen
in Folge enthalten sind. Der Wert ![]() steigt damit sehr stark
an, aber es ist nahezu ausgeschlossen, durch fortgesetzte Simulation
bis zu dieser theoretischen Obergrenze noch eine Verbesserung zu erreichen.
In diesem Fall empfiehlt es sich,
steigt damit sehr stark
an, aber es ist nahezu ausgeschlossen, durch fortgesetzte Simulation
bis zu dieser theoretischen Obergrenze noch eine Verbesserung zu erreichen.
In diesem Fall empfiehlt es sich, ![]() durch einen realistischeren
Wert, z.B.
durch einen realistischeren
Wert, z.B.
![]() zu ersetzen.
zu ersetzen.
Das Verfahren wurde in leicht modifizierter Form für das Faktorisierungsprogramm
qsieve implementiert. In der folgenden Tabelle sind die Ergebnisse
diverser Faktorisierungsläufe, die unter qsieve-2.34 auf
einem Pentium 166-MMX mit verschiedenen Vorfaktoren für die Zahl
![]() = 1607911047862414358613559 (25)
= 1607911047862414358613559 (25) ![]() 189764426443462100134301
(24) durchgeführt wurden, zusammengefaßt. Der zehnstellige Faktor
im Nenner wurde dabei durch das Pollard-Rho-Verfahren in ca. 19 Sekunden
gefunden, die beiden übrigen Faktoren durch das quadratische Sieb.
189764426443462100134301
(24) durchgeführt wurden, zusammengefaßt. Der zehnstellige Faktor
im Nenner wurde dabei durch das Pollard-Rho-Verfahren in ca. 19 Sekunden
gefunden, die beiden übrigen Faktoren durch das quadratische Sieb.
Als Vorfaktoren kommen in der implementierten Fassung nur solche Zahlen
vor, für die
![]() erfüllt ist. Die tatsächlich
verwendete Faktorbasis hatte eine Größe von 1000 Elementen. Es wurden
je ein Lauf mit einem Factor-Threshold von 1.0 (sowohl mit (B) als
auch ohne (C) Berücksichtigung dynamische Faktoren5) und 1.5 (großer Anteil an dynamischen Faktoren (A)) durchgeführt.
Die Vorfaktorbewertungen
erfüllt ist. Die tatsächlich
verwendete Faktorbasis hatte eine Größe von 1000 Elementen. Es wurden
je ein Lauf mit einem Factor-Threshold von 1.0 (sowohl mit (B) als
auch ohne (C) Berücksichtigung dynamische Faktoren5) und 1.5 (großer Anteil an dynamischen Faktoren (A)) durchgeführt.
Die Vorfaktorbewertungen
![]() wurden mit Faktorbasen
der Größe von 75 und 1000 vorgenommen. Der Index
wurden mit Faktorbasen
der Größe von 75 und 1000 vorgenommen. Der Index ![]() gibt dabei den
Typ der Bewertungsfunktion an:
gibt dabei den
Typ der Bewertungsfunktion an:
| Bewertungsfunktion | Beschreibung |
|
|
wie oben definiert, Berücksichtigung von Potenzen |
|
|
wie oben, jedoch werden bei Siebtreffer keine Potenzen berücksichtigt |
|
|
Berücksichtigung von Potenzen und Dirty-Sieving-Effekt |
|
|
keine Berücksichtigung von Potenzen, Berücksichtigung des Dirty-Sieving-Effektes |
In ![]() werden höhere Potenzen von Primzahlen aus der Faktorbasis
vollkommen vernachlässigt. In
werden höhere Potenzen von Primzahlen aus der Faktorbasis
vollkommen vernachlässigt. In ![]() sowie
sowie ![]() wurde
gegenüber
wurde
gegenüber ![]() bzw.
bzw. ![]() der Dirty-Sieving-Effekt6 dadurch berücksichtigt, daß den Primzahlen aus der Faktorbasis, die
der Dirty-Sieving-Effekt6 dadurch berücksichtigt, daß den Primzahlen aus der Faktorbasis, die
![]() teilen, erst dann ein Bonus angerechnet wird, wenn mit
ihnen auch gesiebt wird.7
teilen, erst dann ein Bonus angerechnet wird, wenn mit
ihnen auch gesiebt wird.7
|
|
In der nachfolgenden Tabelle werden die Vorfaktoren für die Faktorisierung
der Zahl
![]() = 5577686387918002774149382469 (28)
= 5577686387918002774149382469 (28) ![]() 52823456865058416450064747 (26) bewertet.
52823456865058416450064747 (26) bewertet.
Die Faktorbasis umfaßte 2000 Elemente, der Factor-Threshold betrug 1.8 und die ersten 5 Elemente der Faktorbasis wurden beim Siebvorgang vernachlässigt, um Zeit zu sparen. Mit Potenzen, die die Siebgröße nicht sprengten, wurde - wie auch im vorigen Beispiel - gesiebt.
| k | Zeit A |
|
|
|
|
|
|
| 7 | 9m44.410s | -5.5967 (5) | -5.3671 (3) | -5.3187 | -5.0891 (3) | -8.9514 | -8.7207 (4) |
| 15 | 7m56.410s (3) | -6.0596 (2) | -5.8555 (2) | -5.3715 (5) | -5.1674 (2) | -9.1485 (5) | -8.9431 (3) |
| 23 | 5m59.990s (2) | -7.6912 (1) | -6.9243 (1) | -7.6912 (1) | -6.9243 (1) | -11.6272 (1) | -10.8590 (1) |
| 31 | 11m44.180s | -4.2522 | -4.1384 | -4.1414 | -4.0276 | -7.9966 | -7.8817 |
| 39 | 13m47.480s | -3.8850 | -3.7487 | -3.3215 | -3.1852 | -7.1155 | -6.9780 |
| 47 | 12m43.800s | -4.7923 | -4.2008 | -4.7923 | -4.2008 | -8.4529 | -7.8603 |
| 55 | 13m36.590s | -3.8666 | -3.7983 | -3.3267 | -3.2585 | -7.0727 | -7.0034 |
| 63* | 10m14.920s | -4.8482 | -4.6187 (5) | -4.2040 | -3.9745 | -7.8522 | -7.6216 |
| 71 | 9m17.650s (5) | -5.4048 | -4.8346 (4) | -5.4048 (3) | -4.8346 (4) | -9.2310 (3) | -8.6595 (5) |
| 79 | 9m56.530s | -4.5392 | -4.3286 | -4.5392 | -4.3286 (5) | -8.4649 | -8.2531 |
| 87 | 14m2.430s | -4.1611 | -3.6787 | -7.3236 | -7.0967 | ||
| 95 | 10m1.320s | -5.2110 | -4.8891 | -8.7181 | -8.1780 | ||
| 143 | 8m47.380s (4) | -5.8008 (4) | -5.3855 (4) | -9.2240 (4) | -8.6058 | ||
| 183 | 9m42.700s | -5.1475 | -8.6128 | -8.2565 | |||
| 207* | 5m55.710s (1) | -5.8602 (3) | -5.4939 (2) | -9.4300 (2) | -9.0280 (2) |
Nicht aus den Tabellen ersichtlich sind die mit steigender zu simulierender
Faktorbasis ansteigenden Simulationslaufzeiten. Das implementierte
Verfahren (mit
![]() ) liefert in allen vier Varianten für
die Praxis brauchbare Ergebnisse. Die Entscheidung, welches Verfahren
in einer konkreten Implementierung des Quadratischen Siebs eingesetzt
werden sollte, bedarf genauer Analysen. Das Entscheidungsverfahren
sollte nach Möglichkeit die implementierten Heuristiken berücksichtigen.
Falls ``Dirty-Sieving'' zum Einsatz kommt und nicht vollständig
mit Potenzen gesiebt wird, sollte eine Variante der Bewertungsfunktion
) liefert in allen vier Varianten für
die Praxis brauchbare Ergebnisse. Die Entscheidung, welches Verfahren
in einer konkreten Implementierung des Quadratischen Siebs eingesetzt
werden sollte, bedarf genauer Analysen. Das Entscheidungsverfahren
sollte nach Möglichkeit die implementierten Heuristiken berücksichtigen.
Falls ``Dirty-Sieving'' zum Einsatz kommt und nicht vollständig
mit Potenzen gesiebt wird, sollte eine Variante der Bewertungsfunktion
![]() vorgezogen werden.
vorgezogen werden.
Eine Verbesserung der Resultate bezüglich der Simulationslaufzeit läßt sich dabei mit folgender Heuristik erreichen:
Zunächst werden mit einer relativ kleinen Faktorbasis die fünf besten Vorfaktoren ermittelt. Nur für diese fünf Werte wiederholt man die Vorfaktorbewertung mit einer größeren Faktorbasis. Der damit ermittelte Vorfaktor wird schließlich übernommen. Zusätzlich kann man die Größe der Simulations-Faktorbasen von der Größe der zu faktorisierenden Zahl bzw. von der Größe der später tatsächlich verwendeten Faktorbasis abhängig machen, um damit die Simulationslaufzeit an die Größe der zu faktorisierenden Zahl zu koppeln.
Die vorgestellten Bestimmungsmethoden optimieren zwar den Vorfaktor, aber für die Optimierung wird die Laufzeit des Quadratischen Siebs weitgehend vernachlässigt. Möglicherweise kann also ein mit diesem Verfahren ermittelter optimaler Vorfaktor bezüglich der tatsächlichen Laufzeit des Quadratischen Siebs suboptimal sein. Für genauere Analysen benötigt man allerdings die Laufzeit verschiedener Siebalgorithmen auch in Abhängigkeit von der Qualität der Faktorbasen. Ob man hier durch theoretische Analysen zu sinnvollen Ergebnissen kommt, darf bezweifelt werden. Auch dürfte ein simulativer Ansatz diesbezüglich erfolgversprechender sein.
Für die in der Praxis häufig auftretenden Fälle dürften die hier vorstellten Verfahren brauchbare Vorfaktoren liefern, zumal sich durch Variation eines Vorfaktors leicht Laufzeitunterschiede um den Faktor zwei und mehr erreichen lassen. Laufzeitunterschiede um den Faktor zwei entsprechen andererseits Schwankungen um drei Dezimalstellen in der zu faktorisierenden Zahl, so daß auch die in seltenen Fällen auftretenden dreistelligen Vorfaktoren nicht zu substantiellen Laufzeitunterschieden führen dürften, selbst wenn kleinere Vorfaktoren bessere Laufzeitresultate aufweisen könnten.
In jedem Fall erweisen sich die vorgestellten Vorfaktorbestimmungsmethoden gegenüber Selektionsverfahren aus konstant vorgegebenen Vorfaktormengen überlegen.
This document was generated using the LaTeX2HTML translator Version 2002-2-1 (1.70)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -transparent -white -antialias -html_version 4.0 -split 0 -nonavigation Vorfaktorbestimmung.tex
The translation was initiated by Thorsten Reinecke on 2003-11-05