Next: 8 Noch eine Berechnungsmethode Up: Über Fibonacci-Folgen Previous: 6 Geschlossene Form Index
Der goldene Schnitt wird allgemein als äußerst harmonisches Verhältnis zweier Seitenlängen zueinander angesehen. Zwei Zahlen stehen im goldenen Schnitt zueinander, wenn sich die Summe beider Zahlen zur größeren Zahl wie die größere Zahl zur kleineren Zahl verhält. Das Verhältnis zweier aufeinanderfolgender Fibonaccizahlen nähert sich dem goldenen Schnitt an.
Berechnen wir zunächst das Verhältnis zweier aufeinanderfolgender Glieder der allgemeinen Fibonaccifolge anhand der geschlossenen Form:
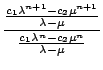 =
= 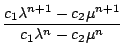 =
= 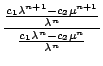 =
= 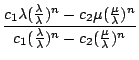 =
= 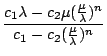
mit
c1 : = (f1 + ![]() ) und
c2 : = (f1 +
) und
c2 : = (f1 + ![]() )
)
Dieser Quotient strebt gegen einen Grenzwert, da
![]()
![]()
![]() =
= ![]()
![]()
![]() =
= ![]() < 1
und daher
< 1
und daher
![]() (
(![]() )n = 0
gilt:
)n = 0
gilt:
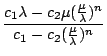 =
= 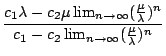 =
= 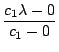 =
= 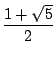
![]() hat einige interessante Eigenschaften, es gilt z.B.:
hat einige interessante Eigenschaften, es gilt z.B.:
(i)
![]() = (
= (![]() )2 =
)2 = ![]() =
= ![]() = 1 +
= 1 + ![]() =
= ![]() + 1
+ 1
(ii) Mit Eigenschaft (i) im Zähler gilt
![]() =
= ![]() =
= ![]() =
= ![]() ;
damit erfüllt
;
damit erfüllt ![]() genau die oben geschilderte Definition des
goldenen Schnitts. Andererseits ist
genau die oben geschilderte Definition des
goldenen Schnitts. Andererseits ist
![]() = 1 +
= 1 + ![]() .
Folglich gilt
1 +
.
Folglich gilt
1 + ![]() =
= ![]() und das ist äquivalent
zu
und das ist äquivalent
zu
![]() =
= ![]() - 1.
- 1.
Diese Eigenschaften folgen auch schon daraus, daß ![]() und
und ![]() die Nullstellen des charakteristischen Polynoms x2 - x - 1 sind.
die Nullstellen des charakteristischen Polynoms x2 - x - 1 sind.
(iii) Ferner gilt
![]() .
. ![]() =
= ![]() .
. ![]() =
= ![]() =
= ![]() = - 1,
also
= - 1,
also
![]() = -
= - ![]() sowie
sowie
![]() = -
= - ![]() .
.
Lassen wir die Fibonaccifolgen für einen Augenblick ruhen und schreiben
die Definition des Goldenen Schnitts nieder, wobei a und b
(mit a > b) unsere zwei Zahlen seien, die im Verhältnis des Goldenen
Schnitts stehen:
![]() =
= ![]() . Wir können diese Gleichung
normieren, indem wir verlangen, daß die kleinere Zahl 1 ist:
. Wir können diese Gleichung
normieren, indem wir verlangen, daß die kleinere Zahl 1 ist:
![]() =
= ![]() .
Setzen wir nun
x : =
.
Setzen wir nun
x : = ![]() , dann erhalten wir daraus die Gleichung
, dann erhalten wir daraus die Gleichung
![]() = x, die (für x
= x, die (für x ![]() 0) zu x + 1 = x2 bzw.
x2 - x - 1 = 0
äquivalent ist. Diese Gleichung haben wir aber bereits in Abschnitt
6 gelöst. Die einzigen Belegungen für x,
die diese Gleichung erfüllen, sind
x =
0) zu x + 1 = x2 bzw.
x2 - x - 1 = 0
äquivalent ist. Diese Gleichung haben wir aber bereits in Abschnitt
6 gelöst. Die einzigen Belegungen für x,
die diese Gleichung erfüllen, sind
x = ![]() und
x =
und
x = ![]() .
.
Für
x = ![]() > 0 können wir folgern: a und b
haben das gleiche Vorzeichen; für
x =
> 0 können wir folgern: a und b
haben das gleiche Vorzeichen; für
x = ![]() < 0 gilt
analog: a und b müssen verschiedene Vorzeichen besitzen. Da
keine weiteren Lösungen existieren, steht zu jeder positiven Zahl
a stets genau die positive Zahl
b : =
< 0 gilt
analog: a und b müssen verschiedene Vorzeichen besitzen. Da
keine weiteren Lösungen existieren, steht zu jeder positiven Zahl
a stets genau die positive Zahl
b : = ![]() im
Verhältnis des Goldenen Schnitts
im
Verhältnis des Goldenen Schnitts
![]() =
= ![]() = a .
= a . ![]() =
= ![]() .
.
Dieses Verhältnis ist eine irrationale Zahl (
![]() = : x
= : x ![]()
![]() ),
woraus folgt: Rationale Zahlen stehen niemals zueinander im Verhältnis
des Goldenen Schnitts. Diese Eigenschaft gilt dann erst recht für
beliebige Teilmengen der rationalen Zahlen, also insbesondere für
die natürlichen Zahlen.
),
woraus folgt: Rationale Zahlen stehen niemals zueinander im Verhältnis
des Goldenen Schnitts. Diese Eigenschaft gilt dann erst recht für
beliebige Teilmengen der rationalen Zahlen, also insbesondere für
die natürlichen Zahlen.
Thorsten Reinecke 2004-07-11