|
Classes |
| class | CDFT_base0 |
| class | CDFT_base |
| class | CDFT |
| class | CDFT_chinrem |
| class | TTempPolynom |
| | a tiny helper class for temporary arrays mpz_t[] in C++ More...
|
Typedefs |
| typedef CDFT_chinrem | TDFT |
| typedef TDFT * | PDFT |
| typedef mpz_t * | TPolynom |
| typedef const mpz_t * | TconstPolynom |
Functions |
| bool | dft_mul_is_recommended (const int k1, const int k2) |
| bool | dft_square_is_recommended (const int k) |
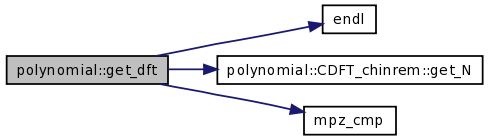
| const PDFT | get_dft (const unsigned int n, const mpz_t m) |
| void | clear_dft_tempmemory () |
| void | print (const TconstPolynom P, int k) |
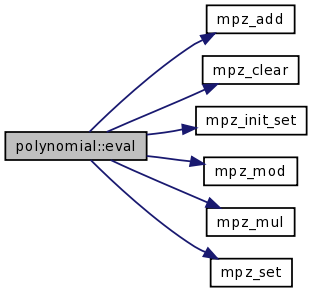
| void | eval (mpz_t res, const TconstPolynom P, const int k, const mpz_t x, const mpz_t m) |
| template<typename T> |
| T | ld (T n) |
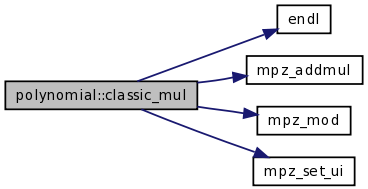
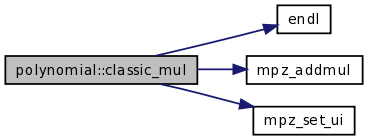
| int | classic_mul (const TPolynom __restrict__ Pr, const int kr, const TconstPolynom P1, const int k1, const TconstPolynom P2, const int k2) |
| int | classic_mul (const TPolynom __restrict__ Pr, const int kr, const TconstPolynom P1, const int k1, const TconstPolynom P2, const int k2, const mpz_t m) |
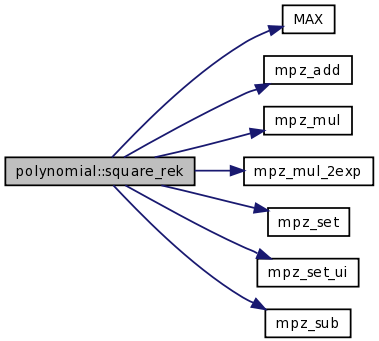
| static int | square_rek (const TPolynom R, const int kR, const TconstPolynom P, const int k, const TPolynom temp) |
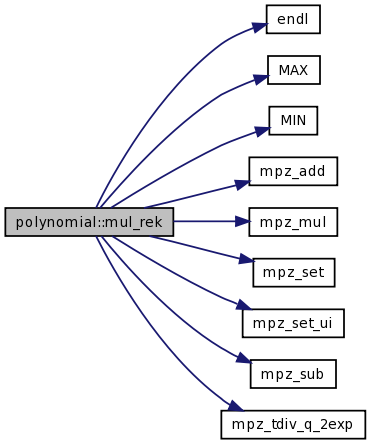
| static int | mul_rek (const TPolynom R, const int kR, const TconstPolynom P1, const int k1, const TconstPolynom P2, const int k2, const TPolynom temp) |
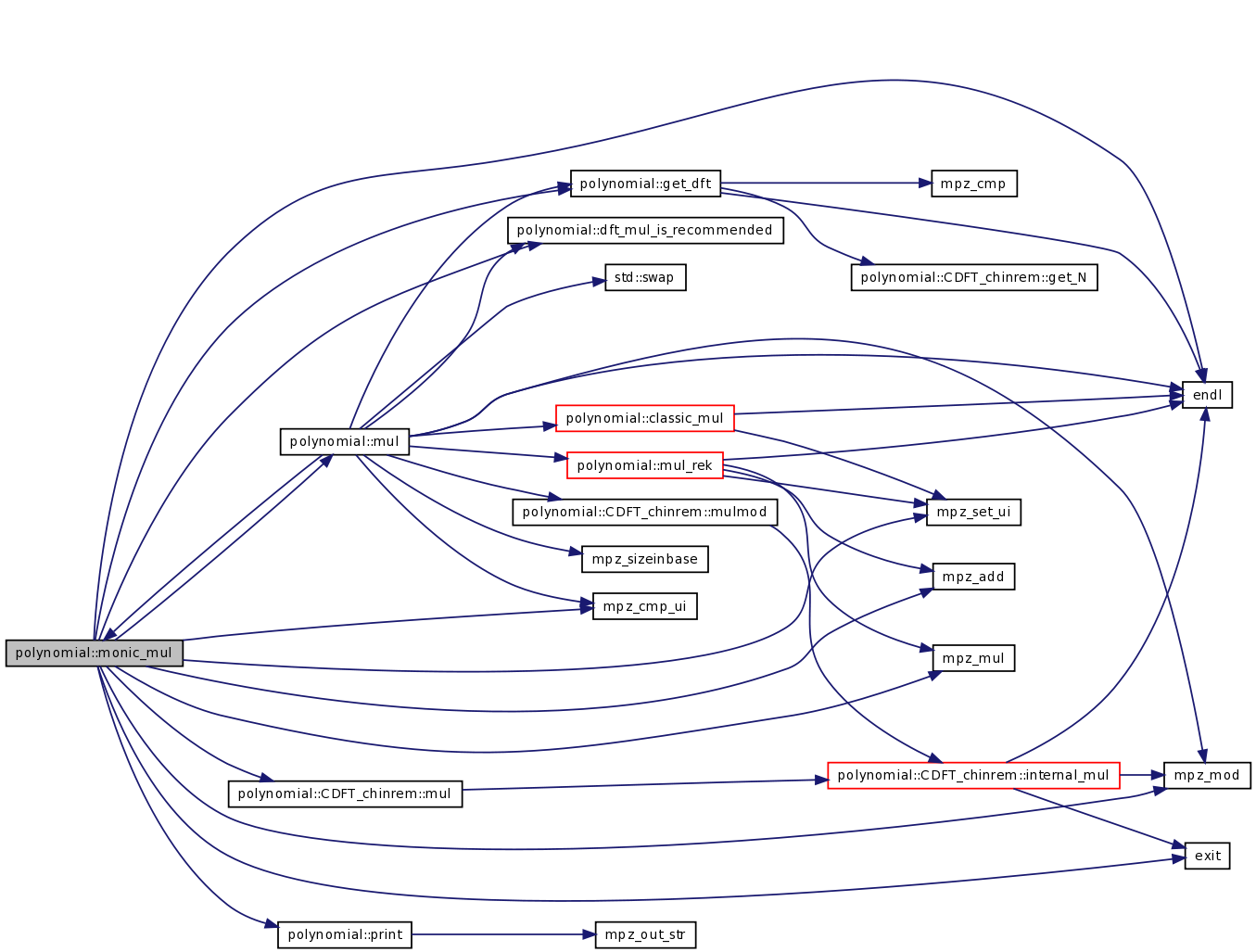
| int | monic_mul (const TPolynom R, const int kR, const TconstPolynom P1, int k1, const TconstPolynom P2, int k2, const mpz_t m) |
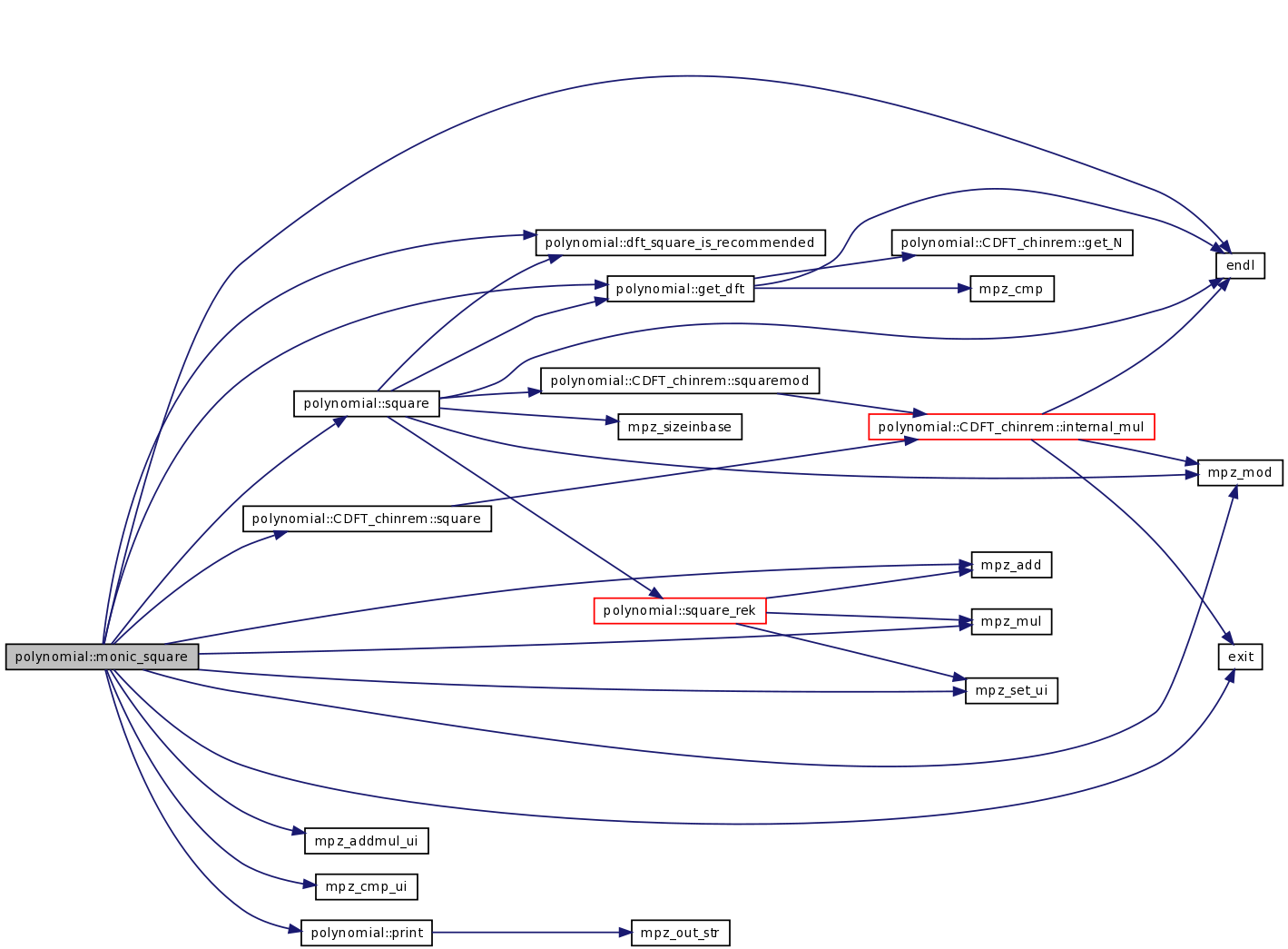
| int | monic_square (const TPolynom R, const int kR, const TconstPolynom P, int k, const mpz_t m) |
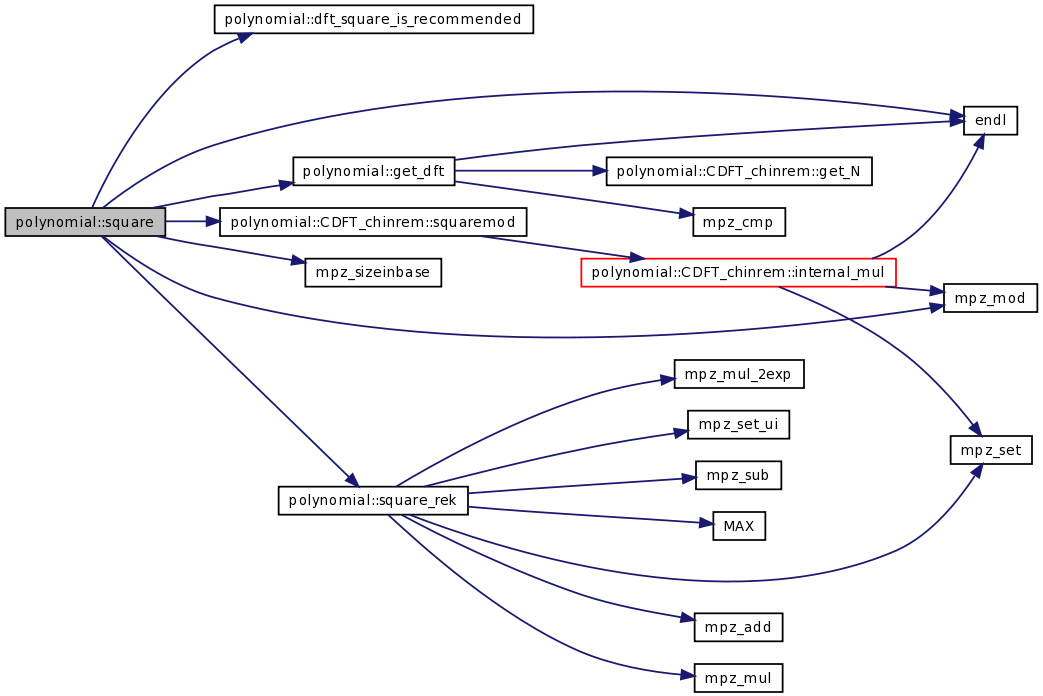
| int | square (const TPolynom R, const int kR, const TconstPolynom P, const int k, const mpz_t m) |
| int | square (const TPolynom R, const int kR, const TconstPolynom P, const int k) |
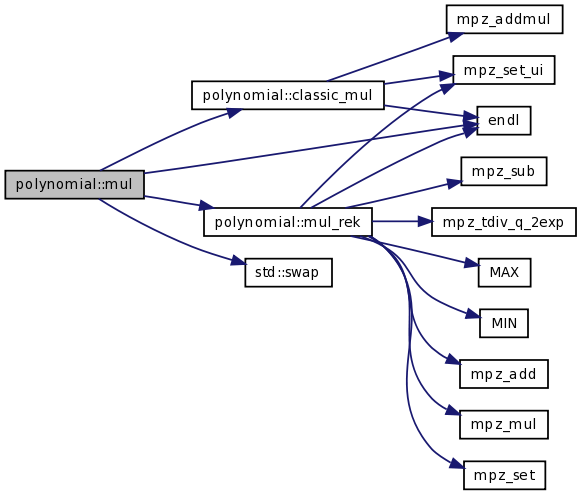
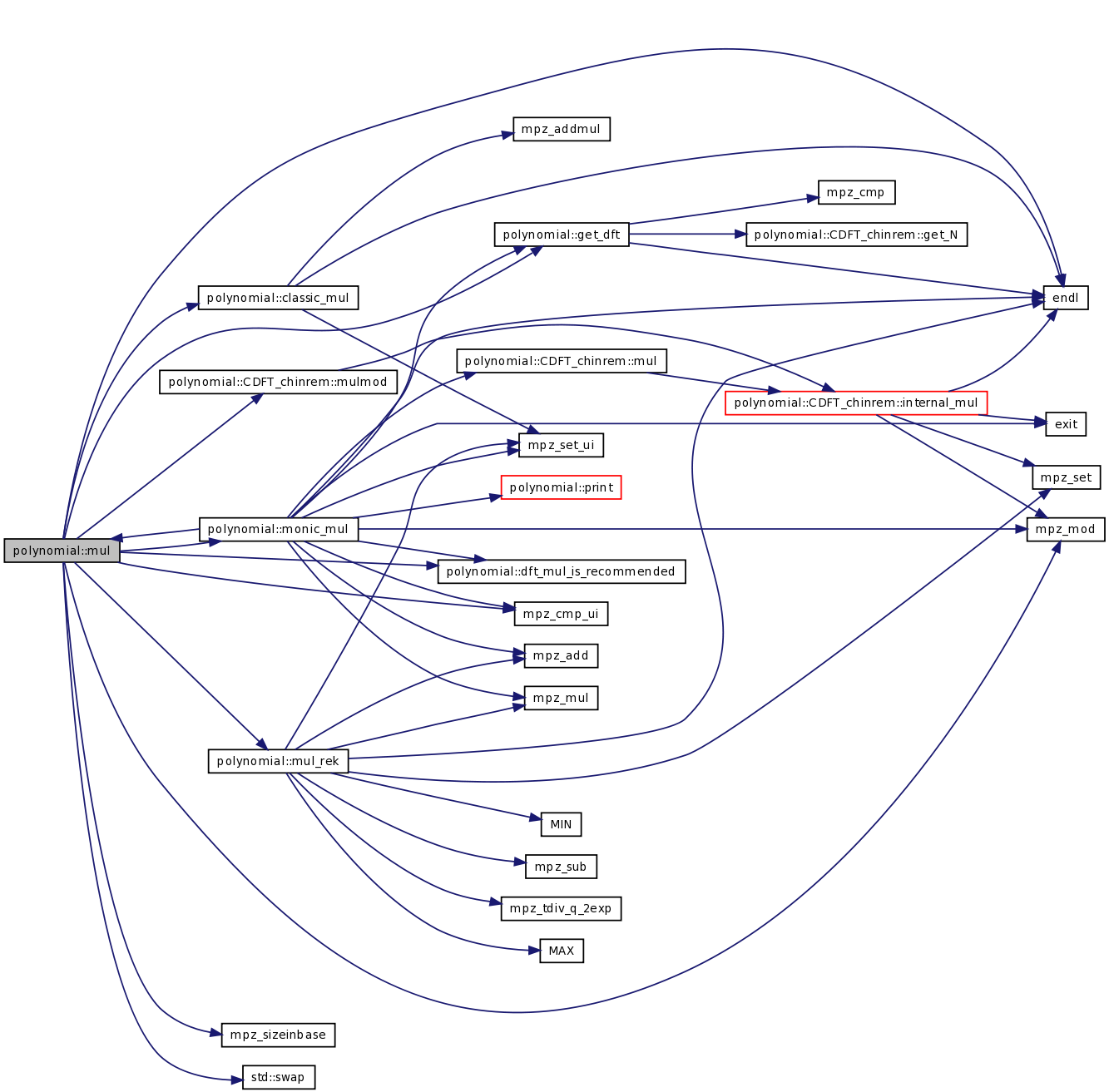
| int | mul (const TPolynom R, const int kR, TconstPolynom P1, int k1, TconstPolynom P2, int k2, const mpz_t m) |
| int | mul (const TPolynom R, const int kR, TconstPolynom P1, int k1, TconstPolynom P2, int k2) |
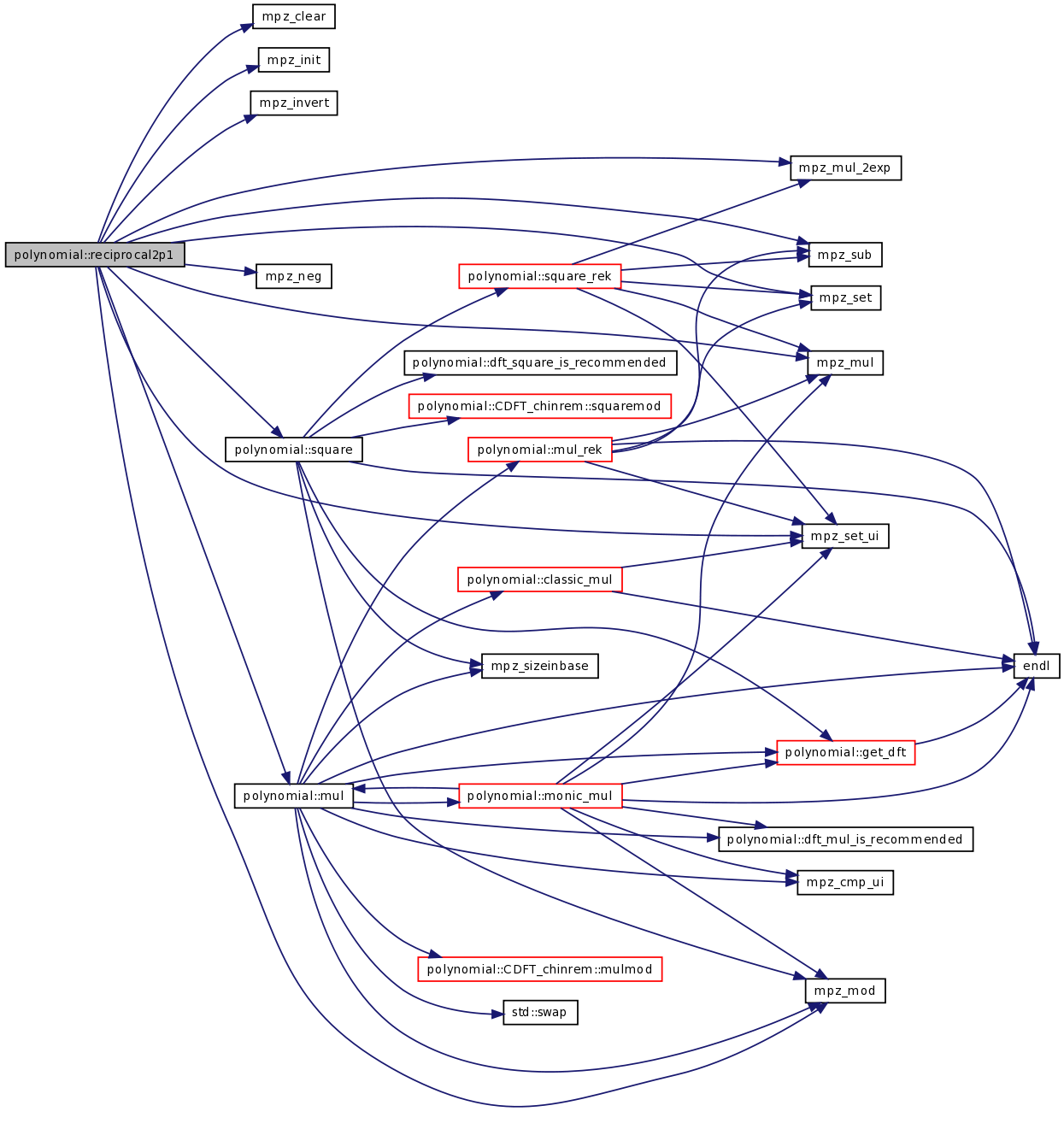
| void | reciprocal2p1 (TPolynom R, int &kR, const TconstPolynom f, const int np1, const mpz_t m) |
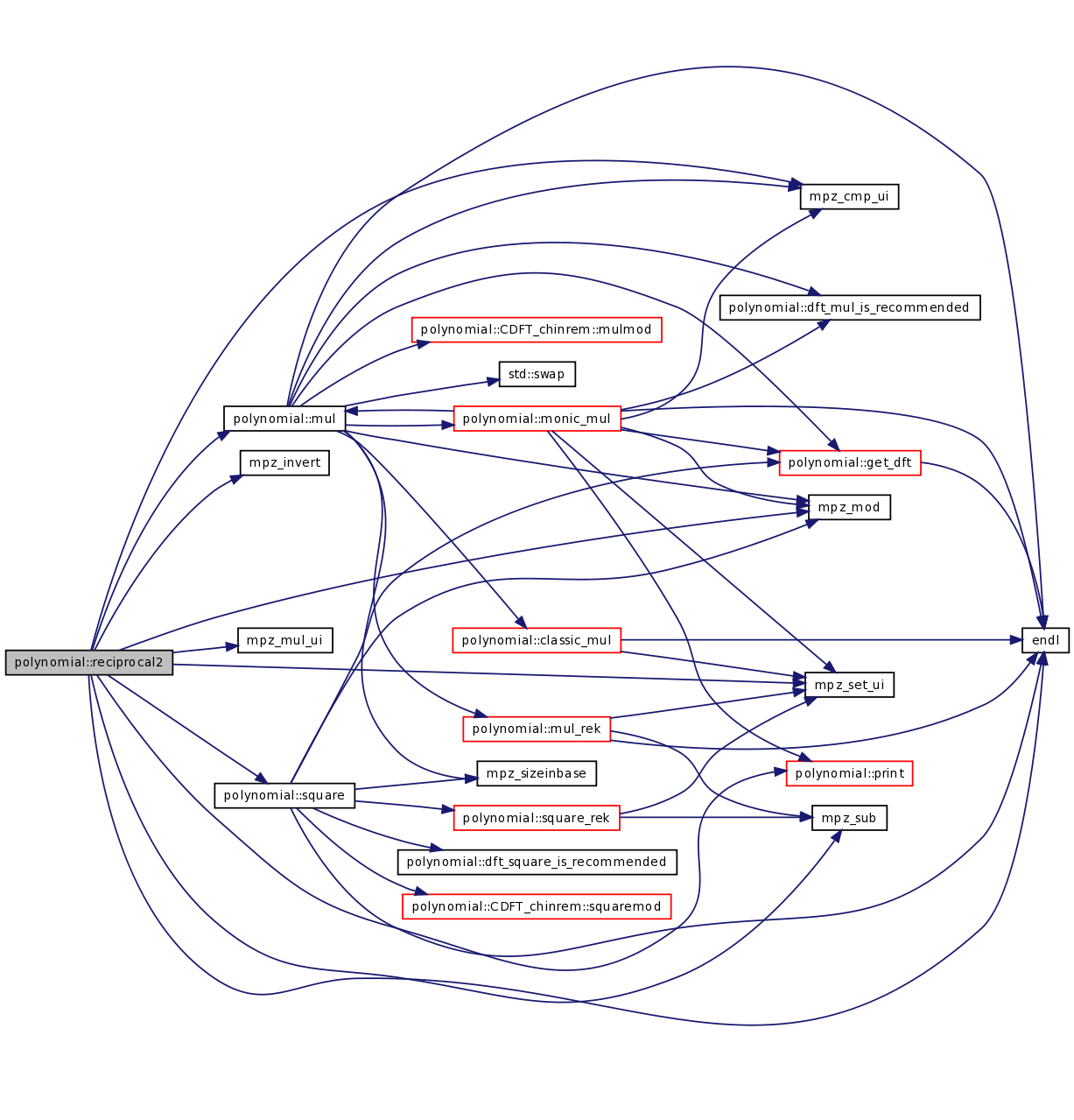
| void | reciprocal2 (TPolynom R, int &kR, const TconstPolynom P, const int k, const mpz_t m) |
| void | reciprocal (TPolynom R, int &kR, const TconstPolynom P, const int k, const mpz_t m, const unsigned int scale) |
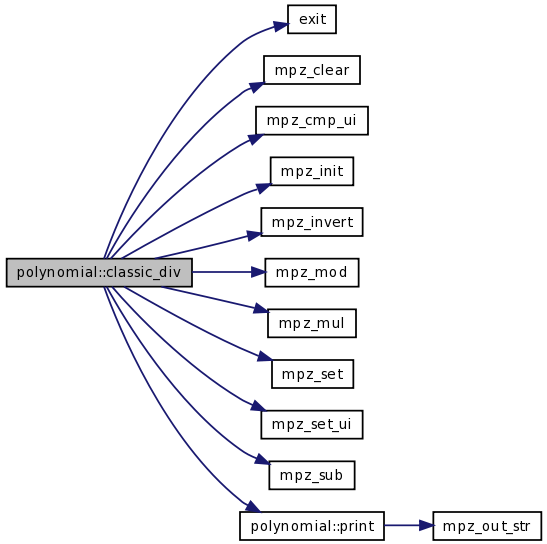
| void | classic_div (TPolynom Q, int &kQ, TPolynom R, int &kR, const TconstPolynom P1, int k1, const TconstPolynom P2, int k2, const mpz_t m) |
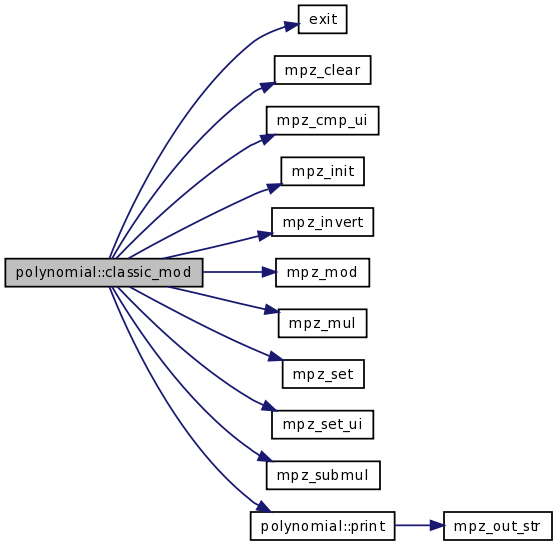
| void | classic_mod (TPolynom R, int &kR, const TconstPolynom P1, int k1, const TconstPolynom P2, int k2, const mpz_t m) |
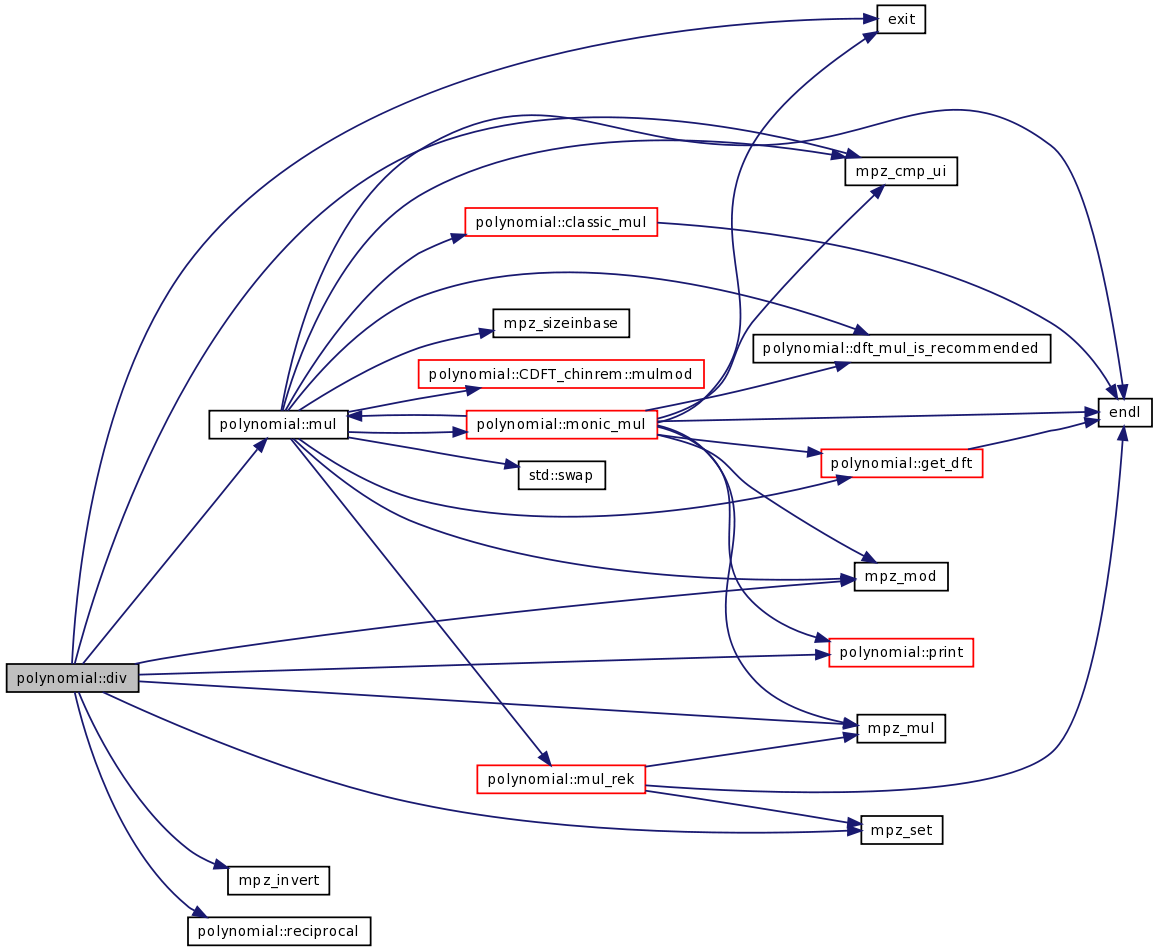
| void | div (TPolynom Q, int &kQ, const TconstPolynom P1, const int k1, const TconstPolynom P2, const int k2, const mpz_t m) |
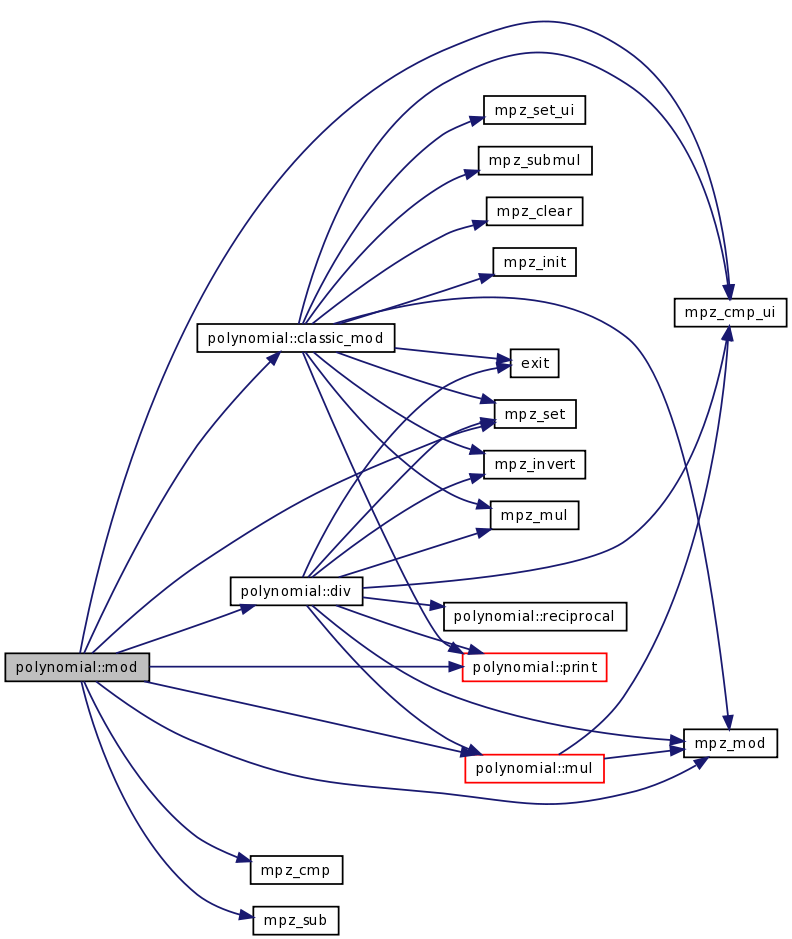
| void | mod (TPolynom R, int &kR, const TconstPolynom P1, int k1, const TconstPolynom P2, int k2, const mpz_t m) |
| static void | multipoint_eval_rek (const TPolynom *R, const TconstPolynom P, const int k, TPolynom *A, const int h, const mpz_t m, mpz_t *&res, int *const pos, const int *const step, const int *const stop) |
| void | multipoint_eval (mpz_t *res, const TconstPolynom P, const int k, const mpz_t *const array_of_arguments, const int size, const mpz_t m) |
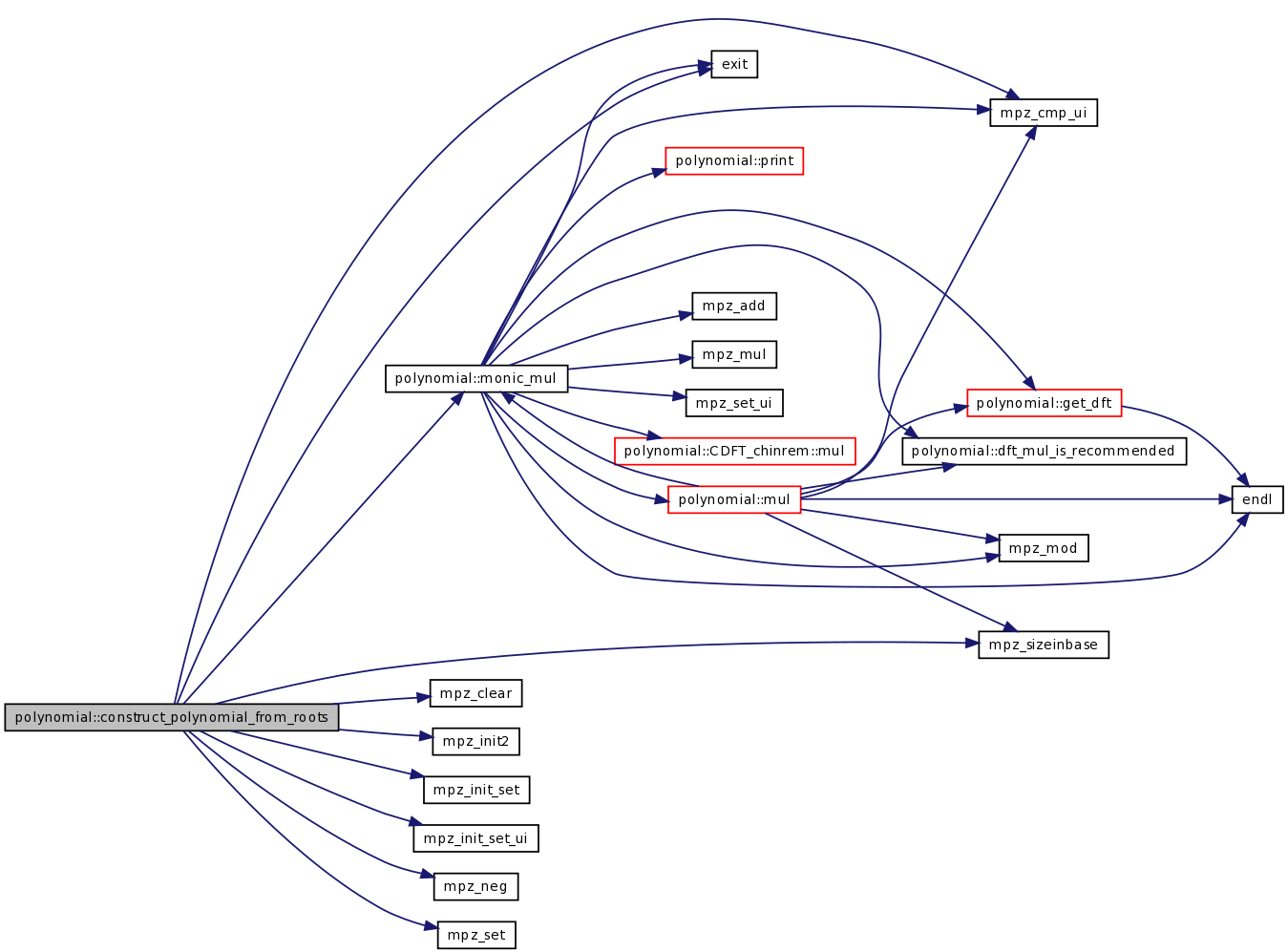
| int | construct_polynomial_from_roots (TPolynom &res, const mpz_t *const roots_array, const int size, const mpz_t m) |
| int | classic_mul (const TPolynom Pr, const int kr, const TconstPolynom P1, const int k1, const TconstPolynom P2, const int k2) |
| int | classic_mul (const TPolynom Pr, const int kr, const TconstPolynom P1, const int k1, const TconstPolynom P2, const int k2, const mpz_t m) |


 1.5.4
1.5.4