polynomial.cc File Reference

contains implementation of polynomial arithmetic for multiple precision numbers More...

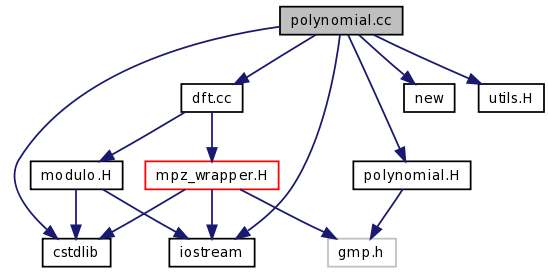
#include <cstdlib>
#include <iostream>
#include <new>
#include "utils.H"
#include "polynomial.H"
#include "dft.cc"

Include dependency graph for polynomial.cc:

This graph shows which files directly or indirectly include this file:

Go to the source code of this file.

Namespaces
namespace	polynomial
Functions
void	polynomial::print (const TconstPolynom P, int k)
void	polynomial::eval (mpz_t res, const TconstPolynom P, const int k, const mpz_t x, const mpz_t m)
template<typename T>
T	polynomial::ld (T n)
int	polynomial::classic_mul (const TPolynom __restrict__ Pr, const int kr, const TconstPolynom P1, const int k1, const TconstPolynom P2, const int k2)
int	polynomial::classic_mul (const TPolynom __restrict__ Pr, const int kr, const TconstPolynom P1, const int k1, const TconstPolynom P2, const int k2, const mpz_t m)
static int	polynomial::square_rek (const TPolynom R, const int kR, const TconstPolynom P, const int k, const TPolynom temp)
static int	polynomial::mul_rek (const TPolynom R, const int kR, const TconstPolynom P1, const int k1, const TconstPolynom P2, const int k2, const TPolynom temp)
int	polynomial::monic_mul (const TPolynom R, const int kR, const TconstPolynom P1, int k1, const TconstPolynom P2, int k2, const mpz_t m)
int	polynomial::monic_square (const TPolynom R, const int kR, const TconstPolynom P, int k, const mpz_t m)
int	polynomial::square (const TPolynom R, const int kR, const TconstPolynom P, const int k, const mpz_t m)
int	polynomial::square (const TPolynom R, const int kR, const TconstPolynom P, const int k)
int	polynomial::mul (const TPolynom R, const int kR, TconstPolynom P1, int k1, TconstPolynom P2, int k2, const mpz_t m)
int	polynomial::mul (const TPolynom R, const int kR, TconstPolynom P1, int k1, TconstPolynom P2, int k2)
void	polynomial::reciprocal2p1 (TPolynom R, int &kR, const TconstPolynom f, const int np1, const mpz_t m)
void	polynomial::reciprocal2 (TPolynom R, int &kR, const TconstPolynom P, const int k, const mpz_t m)
void	polynomial::reciprocal (TPolynom R, int &kR, const TconstPolynom P, const int k, const mpz_t m, const unsigned int scale)
void	polynomial::classic_div (TPolynom Q, int &kQ, TPolynom R, int &kR, const TconstPolynom P1, int k1, const TconstPolynom P2, int k2, const mpz_t m)
void	polynomial::classic_mod (TPolynom R, int &kR, const TconstPolynom P1, int k1, const TconstPolynom P2, int k2, const mpz_t m)
void	polynomial::div (TPolynom Q, int &kQ, const TconstPolynom P1, const int k1, const TconstPolynom P2, const int k2, const mpz_t m)
void	polynomial::mod (TPolynom R, int &kR, const TconstPolynom P1, int k1, const TconstPolynom P2, int k2, const mpz_t m)
static void	polynomial::multipoint_eval_rek (const TPolynom *R, const TconstPolynom P, const int k, TPolynom *A, const int h, const mpz_t m, mpz_t *&res, int *const pos, const int *const step, const int *const stop)
void	polynomial::multipoint_eval (mpz_t *res, const TconstPolynom P, const int k, const mpz_t *const array_of_arguments, const int size, const mpz_t m)
int	polynomial::construct_polynomial_from_roots (TPolynom &res, const mpz_t *const roots_array, const int size, const mpz_t m)

---

Detailed Description

contains implementation of polynomial arithmetic for multiple precision numbers

references and related literature:

[1] Alfred V. Aho, John E. Hopcroft, Jeffrey D. Ullman: "The Design and Analysis of Computer Algorithms", Addison-Wesley, 1974

[2] Robert Sedgewick: "Algorithmen", Addison-Wesley, 1991

[3] Peter L. Montgomery: "An FFT Extension of the Elliptic Curve Method of Factorization", (dissertation, University of California), 1992, ftp.cwi.nl/pub/pmontgom/ucladissertation.psl.gz

Definition in file polynomial.cc.

---