Next: 4 Folgenwerte von Summen Up: Über Fibonacci-Folgen Previous: 2 Grundlegendes Index
Wir betrachten nun den Fall
fn+k + fn-k für k : = 2j und
n ![]() k.
k.
hier haben wir eine »Nullsumme« ergänzt, um nun den Fall k=2 anzuwenden!
und erneute Anwendung ergibt
Wir definieren nun die Koeffizienten c2 : = 3 , c4 : = 7. Doch wie sehen die Koeffizienten für höhere Zweierpotenzen aus? - Nun, diese lassen sich induktiv bestimmen:
Wir halten also fest:
Stellt man das vorige Ergebnis um, so erhalten wir fn = c2jfn-2j - fn-2 . 2j = c2jfn-2j - fn-2j+1; hiermit lassen sich rekursiv bereits die Folgenwerte von Zweierpotenzen effizient ermitteln.
Für andere Werte als Zweierpotenzen mag es angebracht sein, den Term
erneut aufzulösen, um das Auftreten negativer Indices zu vermeiden.
Zur Vereinfachung der Schreibweise wählen wir für ein gegebenes n
ein eindeutig bestimmtes k mit der Eigenschaft
![]() < k : = 2j
< k : = 2j ![]()
![]() .
Dann gilt:
.
Dann gilt:
Bisher haben wir den Wert k = 1 bei den obigen Betrachtungen ausgeklammert. Er scheint auch zunächst nicht sonderlich hilfreich zu sein. Bei der Berechnung von fn können wir ja vorzeitig abbrechen und mit der »normalen« Rekursion fn : = fn-1 + fn-2 fortfahren, lange bevor der Fall k = 1 relevant werden würde.
Trotzdem sei der Fall der Vollständigkeit halber erwähnt:
Eine im Augenblick noch nicht direkt anwendbare, aber interessante Eigenschaft tritt zutage, wenn wir die Fibonaccifolge betrachten: Fn+1 + Fn-1 = Ln. Sie haben richtig gelesen, dies ergibt die Lucasfolge!3 Und diese Behauptung gilt es zu beweisen. Das geschieht in zwei Schritten:
Zunächst betrachten wir, ob die Startwerte übereinstimmen:
L0 = 2, F0+1 + F0-1 = F1 + F-1 = 1 + 1 = 2
L1 = 1, F1+1 + F1-1 = F2 + F0 = 1 + 0 = 1
Die Startwerte stimmen also überein. Der Wert von F-1 kann nämlich folgerichtig anhand der Rekursionsgleichung Fn = Fn-1 + Fn-2 für n = 1 ermittelt werden: F1 = F0 + F-1, also F-1 = F1 - F0 = 1 - 0 = 1.
Im zweiten Schritt sollte noch gezeigt werden, daß die Folge Fn+1 + Fn-1 auch tatsächlich der Rekursionsgleichung Ln = Ln-1 + Ln-2 genügt:
Wenn wir die Koeffizienten aus 3.3 betrachten und ihnen
die zugehörigen Lucasfolgenwerte gegenüberstellen, so kommen wir auf
die Vermutung, daß diese für j ![]() 1 gleich sind.
1 gleich sind.
c21 = c2 = 3 sowie L21 = L2 = L1 + L0 = 1 + 2 = 3
c22 = c4 = 7 sowie L22 = L4 = L3 + L2 = L2 + L1 + L2 = 3 + 1 + 3 = 7
Unter Anwendung von der Gleichung aus 3.4 bestätigt sich diese Vermutung:
Mit
c2j+1 : = c2j2 - 2 für j ![]() 1 einerseits, und
L2j+1 = c2jL2j+1-2j - L2j+1-2 . 2j = c2jL2j - L0 = c2jL2j - 2
anderseits folgt mit der Induktionsannahme
L2j = c2j
auch
L2j+1 = c2jL2j -2 = c2jc2j -2 = c2j2 -2 = c2j+1
für alle folgenden Zweierpotenzen.
1 einerseits, und
L2j+1 = c2jL2j+1-2j - L2j+1-2 . 2j = c2jL2j - L0 = c2jL2j - 2
anderseits folgt mit der Induktionsannahme
L2j = c2j
auch
L2j+1 = c2jL2j -2 = c2jc2j -2 = c2j2 -2 = c2j+1
für alle folgenden Zweierpotenzen.
Wir halten also fest:
L2j+1 = c2j+1 = L2j2 - 2 für j ![]() 1
1
Lösen wir uns jetzt von den Zweierpotenzen, so daß k nun beliebige Werte annehmen kann. Betrachten wir zunächst zwei weitere Beispiele, wobei wir das Vorzeichen variieren.
Wenn man die Koeffizienten mit den Werten der Lucasfolge vergleicht, kommt man nach einigem hin- und her vielleicht auf die Idee: Lk ist für gerade k bei der Summe und für ungerade k bei der Differenz der zugehörige Koeffizient.
Mithin vermutet man: fn+k + (- 1)kfn-k = Lk . fn
Diese Vermutung gilt es nun zu beweisen. Dies geschieht per Induktion über k.4
Induktionsannahme: Für k> 0 sei sowohl für k - 1 als auch für k die Behauptung erfüllt. Zu zeigen bleibt, daß sie dann auch für k + 1 erfüllt ist, und somit induktiv aufsteigend für alle k + i durch den beliebig oft wiederholbaren Übergang von k auf k + 1 (vollständiges Induktionsprinzip).
Für n = 0 erhalten wir mit obigem Satz
Die Anwendung des obigen Satzes auf f : = L ergibt Ln+k + (- 1)k . Ln-k = Ln . Lk, somit ergibt sich Ln+k = LnLk - (- 1)kLn-k.
Setzen wir nun noch k : = n, so erhalten wir Ln+n = Ln . Ln - (- 1)kLn-n = Ln2 - (- 1)nL0, also L2n = Ln2 - (- 1)n . 2. Dies ist eine Verallgemeinerung des in 3.5.3 ermittelten Resultats.
Wir wenden zunächst 3.6.5 für L2n+n und später 3.6.6 an:
Die nachfolgende Herleitung ist typisch für die Mathematik. Natürlich hätten wir die Formel auch vom Himmel fallen lassen und anschließend beweisen können. Aber durch einen gezielt gewählten Umweg stößt man häufig auf die gewünschte Abkürzung. So findet das Schiff den Weg in die Flasche:
Wir betrachten f : = F sowie die Fälle fn+k und fk+n und erhalten hieraus Fn+k = LkFn - (- 1)kFn-k sowie Fk+n = LnFk - (- 1)nFk-n.
Summation ergibt:
Unter Berücksichtigung der Eigenschaft Fk-n = F-(n-k) = (- 1)(n-k)+1Fn-k erhalten wir
Also
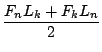
Diesen Fall betrachten wir später noch einmal, trotzdem springt er uns hier schon ins Auge:
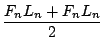 = FnLn
= FnLn
Mit 3.6.3 erhalten wir Fn-k = (- 1)k . (LkFn - Fn+k). Also
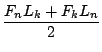 ) =
) = 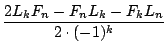 =
= 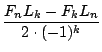
(Alternativ hätten wir auch
Fn-k = Fn+(-k) = ![]() mit anschließender Anwendung von 2.3.1 sowie 2.3.2
ausrechnen können.)
mit anschließender Anwendung von 2.3.1 sowie 2.3.2
ausrechnen können.)
Manchmal fallen Formeln vom Himmel und sind dann zu beweisen. Dann steht man zunächst ohne jede Idee da und staunt (oder ärgert sich). Wenn man sich jedoch die Zeit nimmt, die fallenden Regentropfen zu betrachten, die schließlich als Schneeflocken auf die Erde fallen und den Boden mit einem weißen Mantel überdecken, dann bekommt man eine Ahnung davon, daß auch diese wunderbare Schönheit »nur« eine andere Form des Wassers ist...
Thorsten Reinecke 2004-07-11