Next: 5 Teilbarkeiten Up: Über Fibonacci-Folgen Previous: 3 Summen von Folgenwerten Index
Wenn wir uns die Koeffizienten näher betrachten, sehen wir, daß es Fibonacci-Zahlen sind; also notieren wir sie auch als solche...
Nun spezialisieren wir für i = j :
Wir halten dieses Ergebnis für den allgemeinen Fall dieser zweistufigen Rekursionsfolgen fest!
Eine nicht minder interessante Spezialisierung erhalten wir für i = k + j - 1:
Wenn wir nun noch n : = k + j substituieren, erhalten wir fn = Fnf1 + Fn-1f0, und das ist fürwahr ein gelungenes Ergebnis!
f2n = fn+n = Fn+1 . fn + Fn . fn-1 (mit 4.1.1)
Alternativ erhalten wir unter Anwendung von 3.6.3 fn+n = Ln . fn - (- 1)nfn-n, also f2n = Ln . fn - (- 1)n . f0.
Nun spezialisieren wir die obigen Fälle auf die Fibonacci-Folge, setzen also f : = F.
F2n = Fn+1Fn + Fn . Fn-1
= Fn . (Fn+1 + Fn-1) = Fn . Ln (mit 3.5.2)
Dies halten wir als Ergebnis fest, rechnen aber trotzdem weiter:
= (Fn+1 - Fn-1)(Fn+1 + Fn-1)
= Fn+12 - Fn-12
Somit erhalten wir den Satz:
Mit 4.2 sowie 3.6.6 erhalten wir:
Rechnen wir mit obigem Ergebnis weiter:
und unter Anwendung von 4.3
somit:
Außerdem ergibt sich wegen Ln = Fn+1 + Fn-1 interessantes:
also (und dies gilt es festzuhalten!):
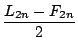 =
= 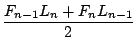
(Dasselbe Ergebnis hätten wir auch unter Verwendung von 3.6.8 für F-1+2n sowie F(n-1)+n erhalten.)
Unter Anwendung von 3.6.3 erhalten wir
Thorsten Reinecke 2004-07-11