Next: 10 Ein »einfacher« Faktorisierungsalgorithmus Up: Über Fibonacci-Folgen Previous: 8 Noch eine Berechnungsmethode Index
Wir verwenden die Eigenschaft aus Abschnitt 8, dann erhalten wir einerseits
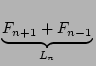
Abschließend für die Betrachtung des Terms
![]() sei der
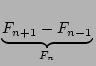
Vollständigkeit halber noch auf eine dritte Umformungsvariante hingewiesen:
sei der
Vollständigkeit halber noch auf eine dritte Umformungsvariante hingewiesen:
 ) . (
) . ( ),
doch diese Formel kennen wir mit anderer Herleitung bereits aus Abschnitt
4.3.
),
doch diese Formel kennen wir mit anderer Herleitung bereits aus Abschnitt
4.3.
Auch auf die Gefahr hin, nun vollkommen zu langweilen, wenden wir das obige Prinzip aus 9.1 erneut an, diesmal um eine Formel für Fk . n zu bestimmen:
Als möglicherweise noch recht interessantes Beispiel der Anwendung obiger Formel können wir F3n betrachten. Es ergibt sich zum einen
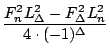
Wir verwenden die geschlossene Form. Somit ergibt sich einerseits
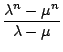 )2 - (- 1)n+
)2 - (- 1)n+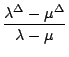 )2
)2
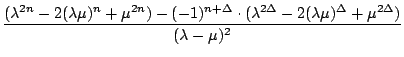 = *
= *
( Hinweis:
![]() .
. ![]() =
= ![]() .
. ![]() =
= ![]() =
= ![]() = - 1
)
= - 1
)
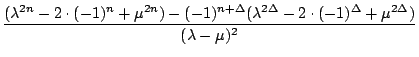
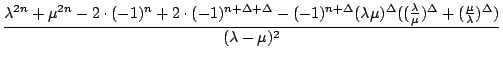
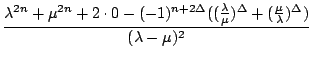 =
= 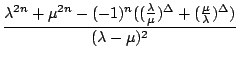 = : h
= : h
und andererseits
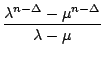 .
. 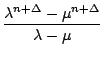 =
= 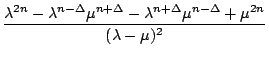
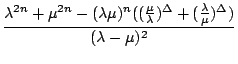 =
= 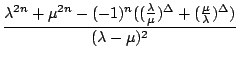 = h
= h
Da beide Terme gleich sind, ist der erste Teil der Formel korrekt. Für den letzten Teil ergibt sich mit 3.6.8 und 3.6.9:
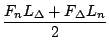 .
. 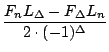 =
= 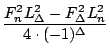
![]()
Bevor wir die eigentliche Formel vorstellen und mit dem Induktionsbeweis beginnen, folgt zunächst ein kleiner Hilfssatz.
(i) aus
(![]() )2 = (Fn2 +2FnFn-1)
)2 = (Fn2 +2FnFn-1)![]() + Fn2 + Fn-12
folgt
F2n = Fn2 +2FnFn-1
+ Fn2 + Fn-12
folgt
F2n = Fn2 +2FnFn-1
(ii) aus
![]() =
= ![]() .
. ![]() folgt
F2n = Fn-
folgt
F2n = Fn-![]() Fn+
Fn+![]() + Fn-
+ Fn-![]() Fn-1+
Fn-1+![]() + Fn-1-
+ Fn-1-![]() Fn+
Fn+![]()
Aus (i) und (ii) in Verbindung mit Formel 9.3 folgt
und daraus folgt die obige Gleichung.
Nach dieser Vorarbeit kommen wir nun zu unserer Formel
Der Induktionsanker ![]() = 0 ergibt
FnFn-1 = FnFn-1 + (- 1)n . 0
und ist daher erfüllt. Sei nun die Behauptung für
= 0 ergibt
FnFn-1 = FnFn-1 + (- 1)n . 0
und ist daher erfüllt. Sei nun die Behauptung für ![]() wahr.
Zu zeigen bleibt die Korrektheit der Behauptung für
wahr.
Zu zeigen bleibt die Korrektheit der Behauptung für ![]() + 1:
+ 1:
| Fn-( |
|
= Fn-1-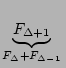 F F |
|
= Fn-1-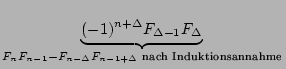 - (- 1)n+ - (- 1)n+ |
|
= 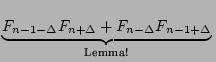 - FnFn-1 - (- 1)n+ - FnFn-1 - (- 1)n+ |
|
| = 2FnFn-1 + (- 1)n+ |
|
| = FnFn-1 |
q.e.d.
Erinnern wir uns einerseits noch einmal an die Binetsche Formel
Fn = ![]() aus Abschnitt 6. Dabei wurde
aus Abschnitt 6. Dabei wurde
![]() : =
: = ![]() und
und
![]() : =
: = ![]() gesetzt. Erinnern wir uns andererseits
daran, daß es für Periodizitätsbetrachtungen häufig sinnvoll ist,
in Restklassen zu rechnen. - Nun können wir die berechtigte Frage
stellen: Ist es möglich, die geschlossene Form innerhalb einer Restklassenbetrachtung
zu verwenden?
gesetzt. Erinnern wir uns andererseits
daran, daß es für Periodizitätsbetrachtungen häufig sinnvoll ist,
in Restklassen zu rechnen. - Nun können wir die berechtigte Frage
stellen: Ist es möglich, die geschlossene Form innerhalb einer Restklassenbetrachtung
zu verwenden?
Diese Frage führt uns unmittelbar zu dem Problem, ob der Ausdruck
![]() in den Restklassen, die wir betrachten wollen, auf sinnvolle
Weise definiert werden kann.
in den Restklassen, die wir betrachten wollen, auf sinnvolle
Weise definiert werden kann.
Für die nachfolgende Betrachtung benötigen wir Wissen aus der Zahlentheorie,
das z.B. bei [FrIs92] nachgeschlagen werden kann. Zum einen benötigen
wir den sogenannten kleinen Fermatschen Satz, der für Primzahlen p
und teilerfremde Basen a die Folgerung
ap-1 ![]() 1 ( mod p)
aufstellt. Zum anderen benötigen wir einige zentrale Eigenschaften
über quadratische Reste.
1 ( mod p)
aufstellt. Zum anderen benötigen wir einige zentrale Eigenschaften
über quadratische Reste.
Betrachten wir Primzahlen p > 5 und die Primkörper
![]() p,
d.h. die Körper, die bei den Restklassenbetrachtungen modulo Primzahlen
p entstehen. Die unter Abschnitt 6 hergeleitete
geschlossene Form bleibt in solchen Primkörpern gültig, wenn 5
ein quadratischer Rest modulo p ist, mit Hilfe des Legendresymbols
ausgedrückt also
(
p,
d.h. die Körper, die bei den Restklassenbetrachtungen modulo Primzahlen
p entstehen. Die unter Abschnitt 6 hergeleitete
geschlossene Form bleibt in solchen Primkörpern gültig, wenn 5
ein quadratischer Rest modulo p ist, mit Hilfe des Legendresymbols
ausgedrückt also
(![]() ) = 1 gilt; nur dann ist Kongruenz
x2
) = 1 gilt; nur dann ist Kongruenz
x2 ![]() 5 ( mod p)
in
5 ( mod p)
in
![]() p erfüllbar und wir können für unsere
Betrachtung z.B.
p erfüllbar und wir können für unsere
Betrachtung z.B. ![]() als die »größere« und -
als die »größere« und - ![]() als die »kleinere« Lösung dieser Kongruenz definieren.
als die »kleinere« Lösung dieser Kongruenz definieren.
Für Primzahlen p mit
(![]() ) = 1 gilt somit aufgrund des
kleinen Fermatschen Satzes
) = 1 gilt somit aufgrund des
kleinen Fermatschen Satzes
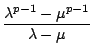
sowie
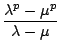
Damit gilt
(Fp-1, Fp) ![]() (0, 1)
(0, 1) ![]() (F0, F1), mithin
gilt die Periodizität
Fk . (p-1)+
(F0, F1), mithin
gilt die Periodizität
Fk . (p-1)+![]()
![]() F
F![]() ( mod p)
für Primzahlen der obengenannten Form.
( mod p)
für Primzahlen der obengenannten Form.
Insbesondere sind für diese Primzahlen die Fibonacciwerte Fp-1 sowie die Terme Fp-2 - 1, Fp - 1 und Fp+1 - 1 durch p teilbar.
Wegen des quadratischen Reziprozitätsgesetzes gilt für ungerade p
Anstatt alle Fälle für
(![]() ) = 1 zu untersuchen, können wir
uns also auf die Fälle
(
) = 1 zu untersuchen, können wir
uns also auf die Fälle
(![]() ) = 1 beschränken. Eine Restklassenbetrachtung
auf
) = 1 beschränken. Eine Restklassenbetrachtung
auf
![]() 5 (vgl. Tabelle 9)
zeigt uns, daß nur Zahlen der Form 5n, 5n + 1 und 5n + 4 (bzw.
5n - 1) quadratische Reste modulo 5 sind. Da Primzahlen größer als
5 weder durch 5 noch durch 2 teilbar sind, können wir folgern: Primzahlen
mit der Eigenschaft
(
5 (vgl. Tabelle 9)
zeigt uns, daß nur Zahlen der Form 5n, 5n + 1 und 5n + 4 (bzw.
5n - 1) quadratische Reste modulo 5 sind. Da Primzahlen größer als
5 weder durch 5 noch durch 2 teilbar sind, können wir folgern: Primzahlen
mit der Eigenschaft
(![]() ) = 1 und p > 5 haben die Form
p = 10 . n±1.
(Diese Form enthält diejenigen quadratischen Reste modulo 10, die
zu 10 teilerfremd sind.)
) = 1 und p > 5 haben die Form
p = 10 . n±1.
(Diese Form enthält diejenigen quadratischen Reste modulo 10, die
zu 10 teilerfremd sind.)
|
|
Für Primzahlen der Form p = 10 . n±1 sind die Terme Fp-2 - 1, Fp-1, Fp - 1 und Fp+1 - 1 durch p ohne Rest teilbar.
Die nicht-quadratischen Reste modulo 10, die zu 10 teilerfremd sind,
haben die Form
10 . n±3. Für Primzahlen dieser Form gilt:
Die Periode Pp (für
Fk . Pp+![]()
![]() F
F![]() ( mod p))
ist ein Vielfaches von p + 1 und es gilt
Fp+1
( mod p))
ist ein Vielfaches von p + 1 und es gilt
Fp+1 ![]() 0 ( mod p).
0 ( mod p).
Ich habe leider keinen Beweis gefunden, der ohne fortgeschrittene Konzepte aus der Zahlentheorie auskommt. Für die erforderlichen zahlentheoretischen Grundlagen sei daher auf [HaRi94], Appendix 4 (The Arithmetic of Quadratic Fields) verwiesen, ohne die der nachfolgende Beweis unverständlich sein dürfte.
Wir betrachten den Körper
![]() (
(![]() ) und setzen
a : = 2 .
) und setzen
a : = 2 . ![]() = 1 +
= 1 + ![]() ,
dann gilt
,
dann gilt
![]() = 1 -
= 1 - ![]() = 2 .
= 2 . ![]() . Wegen
a2 -2a - 4 = (12 +2 .
. Wegen
a2 -2a - 4 = (12 +2 . ![]() +5) - (2 + 2 .
+5) - (2 + 2 . ![]() ) - 4 = 6 - 2 - 4 = 0
sind sowohl a als auch
) - 4 = 6 - 2 - 4 = 0
sind sowohl a als auch ![]() Elemente dieses Körpers.
Elemente dieses Körpers.
Mit der Erweiterung des kleinen Fermatschen Satzes auf solche Körper
gilt
ap ![]()
![]() ( mod p) für
(
( mod p) für
(![]() ) = - 1. Somit
folgt
) = - 1. Somit
folgt
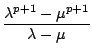 =
= 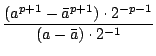 =
= 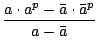 . 2-p
. 2-p
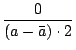 = 0 ( mod p)
= 0 ( mod p)
![]()
Thorsten Reinecke 2004-07-11